Building Number Factories in Beltmatic

10 days ago, I learned about Beltmatic. It came out about a year ago, and describes itself as a casual factory game about mathematics. As a reputed addict of both factory games and mathematics, I got hooked! At least, for as long as it took to get all achievements. This blog post will describe some of the ways I thought about my machines as I built them, and include a few videos and screenshots.

How Beltmatic Works

In a new game of Beltmatic, the game presents you with an infinite square grid. In the center is a 6×6 blue rounded box declaring your current “Level” and the number you need to progress further. At the beginning, you just need to make 1. After you ship 10 copies of the number 1 you will hit level 2, unlock the “adder”, and be able to make progress on your next task.

Along the bottom are the parts you have available. In the beginning, you have “belts” and “extractors”. An extractor will only function if placed in certain places on the board, highlighted with a 3×3 darkened square around a single value. The purpose of the extractor is to give you numbers to work with. Zooming out, you can see that there are a wider variety of numbers out there, but for now the only ones your extractor is able to extract are 1s.

Beltmatic randomizes the map and all of the target values, although they keep the sample range for randomization pretty constrained. The first few levels will always ask for 1, 2, 3, but eventually around 2 digit numbers Beltmatic starts to have variety from one playthrough to the next.

As for the map, you will get the highest density of extractable 1s and 2s near the hub, while the nearest 11 might be 500 tiles away. Later levels unlock new extractable numbers, as well as more factory components.

The Math

Using a 1 extractor to dig up 1s and then ship them as-is, isn’t really math. It is just the 1 = 1 of Beltmatic. Once you have an adder, you can combine numbers and progress to 1 + 1 = 2. Adders do what they say on the package; two values go in, one value comes out equal to the sum of the inputs. The adder takes the shape of a 2×2 square with clear inputs and outputs:

Later in the game, you unlock multiplier, which is a 3×1 rectangle:

Subtractor, which is an L shaped piece:

Divider, which is another square, and does division with remainder:

Exponentiator, which is another L shaped piece:

And finally storage, which just holds up to 10,000 values in a 3×3 box, extractable later:

These are the components with which you can build the number factory of your dreams.

I am Speed

There are certainly many choices in how to build. But here’s where my factory game brain starts thinking about other concepts as well – like throughput.

At base level, each belt moves 2 tiles per second. Numbers each take up one tile on the belt, so this is equivalent to saying that your maximum flow of numbers through any one-tile-wide space is 2 numbers per second. The perimeter of the hub is 24 tiles, so at the base belt level the most optimized your number delivery could possibly be is 48 numbers every second.

This is certainly achievable, even if doing it with base level extractors is silly:

And that potential for silliness is kind of what got me hooked on this game. It is like cycle optimizing Opus Magnum, free to overengineer anything to meet any goal, and where the reward is progressing faster.

Extractor Behavior

Beltmatic measures extractor speed in “belts”. This is clever. You can certainly hook up more belts to an extractor than its top speed, but that results in underfilled belts. For example, here’s 3 belts each filled with one number per 3 tiles:

Extractors are smart enough to notice if a belt is backed up with numbers and can’t accept any more. In this case, it will no longer try to put numbers on that belt, and any other belts get a larger share of the numbers:

An extractor at base level can produce as many values per second as would completely fill one belt. Upgrading your belt indirectly upgrades your extractors, by increasing the number of extracted values per second. Extractors permit direct upgrades too, increasing the number of belts.

Computation Speed

Beltmatic measures addition, as well as every other math operation, in terms of operations per second. This speed applies to a single component, so placing more components permits more operations per second. However, that comes with the difficulty of wiring them all up!

At base level, an adder will do an addition every 4 seconds. Because it uses up 2 input values in the process, it eats 0.5 values per second, which is equal to a quarter of a base level belt. As a result, four adders can perfectly consume values from a filled belt:

However, if you upgrade belts to 2.5 tiles per second, this stops being a perfect match, and now will slowly back up!

This combination of upgrades allows a 5th adder, to reach harmony again. And upgrading the extractor as well to have 2 belts, we can copy paste the setup to double the throughput:

Analysis

The extractor outputs two full belts of 1s, totaling 5 per second. Each 2 is made from a pair of 1s, so if we manage to place enough adders, we can create 2s at 2.5 times per second, which fills one belt. The adder takes 4 seconds per addition, so with 10 additions in parallel, we perform 2.5 additions per second, exactly what we need.

Rearranging it slightly, I could make a single module here that produces a continuous belt of 2s from a 1 extractor, and then copy it 24 times like I had copied the 1s in the “silly” video before. I didn’t quite do that because it is annoying to wire up before unlocking the “bridge” where belts cross over each other, but I did make this:

This became sort of my general pattern for playing. I would build around a single extractor, aiming to completely use all of its possible outputs. I’d compute the relationship between values per second and belt speed, and then copy paste that module as many times as I needed to keep a lot of belts going into the hub.

Things got more interesting with larger target values!

Series and Parallel

To achieve something like 1+1+1+1+1+1+1=7, one needs to wire up adders in series. This allows the output of one adder to be the input of the next. At first, I chose to set up my adders a knight move apart, which mirrored into these triangle shapes:

But eventually I reached the conclusion that a linear layout works better, as you can copy-paste without needing to mirror:

Both of these designs perform 1+1+1+1+1+1+1=7, in two places. Each machine does a serial operation of chained addition, parallelized by using two copies of the chain. However, if we do some analysis, we see that our 12 adders aren’t able to make full use of the extractor. Each branch consumes 7 1s every 4 seconds as the series of adders go off. But we can make 10 1s in that time per belt. This is a case where the best option is to add a third belt, even if the extractor speed is only 2 belts:

This is another win for the linear layout – copying in a third set of adders is basically trivial. Our set of adders now consumes up to 21 values in 4 seconds, while the extractor makes 20. This completely uses the extractor, and because of the automatic balancing between the belts, all 3 of the branches get a proportional number of 1s.

On the output, we make 7 at one-seventh the rate the extractor makes 1s. That comes to a 7 every 1.4 seconds, which isn’t nearly enough to fill a belt. If we copied this 3 times, and converged the outputs on a single belt, it would fill the belt to 85.7%:

Goals

Is it better to achieve 100% of the possible value per extractor, or fill the belt to 100%? Beltmatic doesn’t really care, so it’s a matter of personal preference. Once I have things copy-paste ready, it is so easy to add more copies. So, I prefer to fill the belt to 100%, even if it starts to make less use of the extractors. I’m aware that if I make 7 copies of the module from the previous section, I can split the last copy 50/50 between two belts, and the result would fill both belts to 100%. But, that is a little more work than just making an 8th copy and having 4 copies per belt.

Plus, I want to spend my time designing more modules to hit the other targets! Because Beltmatic starts to ask for more values in order to do upgrades:

At any given time, there can be as many as 19 different target values. 3 to upgrade each upgradable component, and one to upgrade your overall level. Mercifully, when you unlock divider, it shares an upgrade path with subtractor. However, exponentiator does need its own upgrade path, not shown in the above screenshot. The number delivery screen shows all the current values at the hub, along with their purpose.

Sometimes a number becomes useless – I needed to make 335 to upgrade my overall level, but once I did, the requirement changed to 435 and my 335s are now useless. Beltmatic does reuse the values for component upgrades, but only three times each. The goals are ever changing, and so I spent most of my time on module design.

Single Value Problem

I certainly let Beltmatic’s copy-paste feature steer me into a very specific way of playing. I wanted to find a way, for every target, to make it from one extractor. With addition, multiplication, subtraction, and division, that becomes a rather classic math problem. “Write some arbitrary value X in terms of some small value N, and base operations.”

This is like the Four Fours problem, but allowing more instances to make up for not allowing concatenation, square roots, decimal points, or factorials. And so, I ended up having pages and pages of scratch paper full of things like:

• 5222 = (((7 + 7) × 7 + 7) × 7 + 7) × 7 + 7 + 7 + 7 + 7
• 1165 = (((5 + 5) × 5 – 5) × 5 + 5 + 5) × 5 – 5 – 5
• 15300 = ((4 × 4 × 4 – 4) × 4 × 4 – 4) × 4 × 4 + 4
• 4851 = ((7 + 7) × 7× 7 + 7) × 7
• 33749 = ((((5 + 5) × 5 + 5) × 5 – 5) × 5 × 5 × 5 × 5 – 5) ÷ 5

How did I find these, and how do they look as Beltmatic modules?

Finding Them

Wherever possible, I looked to use a divisor of the target value as my starting point. This saved the need for a division step at the end. But sometimes Beltmatic gives out primes! In that case, I would just pick a divisor N of some number close to the target X, and then solve the single value problem for their product N × X.

To solve it, I would start with X, add or subtract N to reach the nearest multiple of N², and then divide the result by N. That looks like this:

Doing the opposite steps in reverse, shows how to build X from N. For example, in the line where 4 becomes 6416, I do the following:

• 6416 is divisible by 16, so divide by 4
• 1604 is not divisible by 16, but 1600 is, so subtract 4
• 1600 is divisible by 16, so divide by 4
• 400 is divisible by 16, so divide by 4
• 100 is not divisible by 16, but 96 is, so subtract 4
• 96 is divisible by 16, so divide by 4
• 24 is not divisible by 16, so subtract 4
• 20 is not divisible by 16, so subtract 4
• 16 is 4 × 4

And so, using multiplication wherever I divided, and addition wherever I subtracted, ((((4 × 4) + 4 + 4) × 4 + 4) × 4 × 4 + 4) × 4 = 6416.

Base N representation

This closely relates to the base N representation of X. Written in base 4, 6416 is (1210100)₄. 4⁶ + 2 × 4⁵ + 4⁴ + 4² = 6416.

Rearranging and factoring out 4s, this can be written as ((((1 × 4) + 1 + 1) × 4 + 1) × 4 × 4 + 1) × 4 × 4 = 6416. The number of 1s added before the next multiplication by 4 is 1, 2, 1, 0, 1, 0, 0. Then distributing the 4 at the end across everything, we reach the exact single-value representation I used.

Since every number has an expression in any base, we know that multiplying and adding gives a way to express anything. At least, so long as the final step is × N so that it can be distributed across all of the 1s. However, sometimes the number of additions gets very large. For example, 2394 = (6660)₇ would be (7 + 7 + 7 + 7 + 7 + 7) × 7 + 7 + 7 + 7 + 7 + 7 + 7) × 7 + 7 + 7 + 7 + 7 + 7 + 7. That’s 20 copies of the number 7, which limits how quickly we can get the result out.

Using subtraction instead, we can include negative numbers in our base N representation, giving what is typically called a “balanced” base-N system. Balanced ternary is the most popular, where the three values are 0, 1, and -1. But we can build a “balanced base-7 representation” for 2394 as (10010)₇ where the strikethrough 1 is the symbol for -1. And this converts to 7 × 7 × 7 × 7 – 7, only 5 copies instead of 20.

Trade-offs

When looking at a given number X, I sometimes got a little bit of decision paralysis for what number I should use as the base. If X didn’t have N as a factor, I would need to build X × N first and then do a final division step, but sometimes that was still better than using a factor that led to a huge number of copies thanks to inconvenient balanced N-ary digits.

I considered writing code to spit out the best choice every time, but I didn’t, at least not during my playthrough. I just scribbled down a couple of the best seeming options and then picked the one with the fewest copies of the number. There were almost certainly better options somewhere I missed. But in general, I found that the sweet spot was bases 3, 4, 5, 6, 7. The problem with 2 (and 1) was that multiplication didn’t make the number big fast enough. The problem with larger bases was that they frequently required a lot of additions or subtractions before the next multiplication.

The highest base I ever chose was 19, after noticing that 8227 = (1440)₁₉ (that’s a negative 4) required only 11 copies of the number 19, which was fewer than any other option I saw. Of course, while writing up the blog post I tried out other values and got another solution in 11 as (((16 + 16) × 16 × 16 + 16 + 16) × 16 + 16 + 16 + 16) ÷ 16 = 8227. Someone could totally write a program for this..

In-game

If I load up my primary save file, I can show this in action for 19553, the next level number:

(By the way, after getting all achievements, I completely deleted my factory. This is something I did at many points through the playthrough as well. The modules serve their purpose. I know other people will tack on expansions, turning old outputs into new inputs. I am not that kind of person. In my factory, we delete and rebuild.)

19553 is a prime number. I’ll choose 7 as the base, since (111002)₇ has small values. I’ll actually be making 136871, and then dividing by 7. I get (((7 × 7 + 7) × 7 + 7) × 7 × 7 × 7 + 7 + 7) ÷ 7 = 19553. 11 copies, not bad. Here’s the process of building the module:

More Analysis

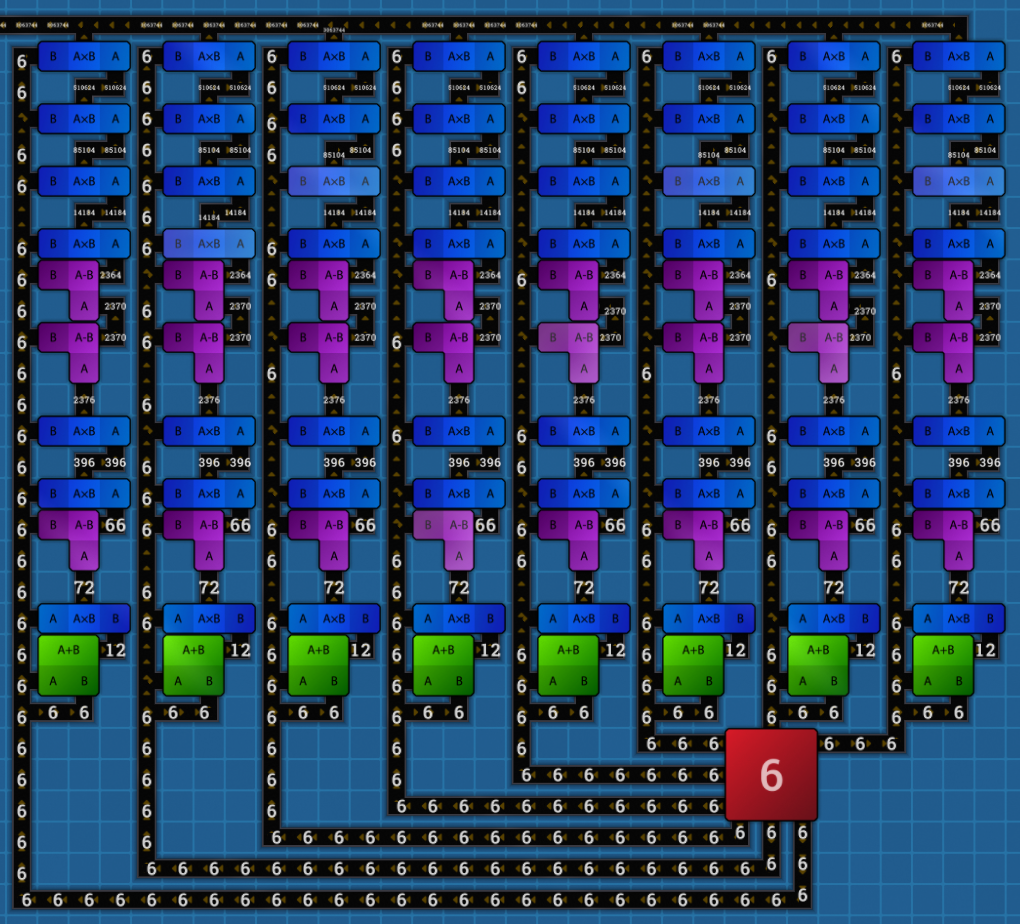
My extractor speed is 8 belts, so for most computations I build 8 copies and wire up one belt to each. A belt can move 8 tiles per second at this level. The multiplier and divider can each act 1 time per second. The adder acts up to 2 times per second, but in this sort of serial design it won’t act any faster than the component that supplies its inputs. So with 11 7s needed to make a 19553, the module is limited by the amount of 7s being extracted, rather than how quickly the math components act.

The extractor puts out 64 7s per second, and once the pieces are in steady state the final belt collects 64 19553s every 11 seconds. That’s less than 8 per second, so I had two modules share a belt to the hub. These then make 100% filled belts, allowing the best possible throughput of 192 values per second, if I copy it enough times.

At one point in the video, I set “belt priorities” using the green diamond. This is a strange feature of Beltmatic I hardly used during my playthrough, but I realized while recording how it makes things better. It allows me to tell Beltmatic that I want the later math operations filled out ahead of time, so that everything gets into the steady state faster. I think it made the initial 19553s come out faster that I set them.

Maximum Silly

Doing a little more crazy wiring, I can get up to 192 values per second.

But I had to do all the wiring while paused, which I didn’t really do in my playthrough. At a paltry 16k requirement, minutes of wiring to save seconds of waiting aren’t worth it. If Beltmatic started to require delivery counts in the millions it would be a different story, but it would also be a less fun game.

Instead, now all of these modules can be deleted! And I can build some other number next.

Achievement Hunting

Among the achievements that Beltmatic offers, are delivering 96 numbers per second, delivering a million numbers total, reaching level 30, and reaching level 8 on all upgrades.

By far the most grueling of these is reaching level 8 on all upgrades. Let me show you what the build targets are for level 9:

A bunch of 5 digit numbers, and for the bottom two, a 6 and even a 7 digit number. Everything in the left two columns was also required to reach level 8, which is why they all have some amount of progress logged.

It’s hilarious to me that the achievement for level 8 is called “reasonably upgraded.” You can see that the amount of benefit for upgrading beyond level 8 is so marginal (except for extractors, for some reason!). By upgrading my adder to level 9, I can achieve another 1% performance, compared to the 50% boost from level 7 to level 8.

Similarly, past level 20 or so, there is not much new unlocked with overall level upgrades. You get the ability to extract larger numbers, which maybe helps some playstyles but not really mine. The sweet spot is 3, 4, 5, 6, 7 after all.

Times I Did Something Different

There was exactly one time I used the exponentiator in my playthrough. The target value was 16389, and I noticed how close it was to 16384 = 2¹⁴. I found a spot with 2, 14, and 5 all available to extract somewhat close to each other, and built this:

Although this let me make 16389 from a smaller number of pieces, I did find relying on multiple different extractors a little awkward. I couldn’t copy paste it, so I only built the one and pumped them into storage. (At the time, this was a future level target, so the play is to store them until the hub is ready to accept them. You can also make massive zig-zag tracks full of a value, if you haven’t unlocked storage yet).

There was also one time that I was building 3354 = (1720)₁₃ where I got annoyed by the 7 and just piped in a 7 manually, rather than using 7 more copies of the number 13. That appears in two copies on the left of the screenshot below, which otherwise shows a representative chunk of my factory during my playthrough:

Other Crazy Ideas

I never used the fact that the divider also supports remainder. I know that this could then be turned into a feedback loop, even one that produces a pseudorandom number stream. The idea of getting every possible output from a single small factory does tickle me, but not enough to set it up (plus, actually making 50k of some random large number would take so long).

I did see one steam reviewer complain that there wasn’t a number disposal. I suppose some playstyles would lament that fact, but there is the option to pump into storage and then periodically use the C hotkey to clear all numbers from the area, including vacating storage. If it were me, I would simply delete the part of the factory responsible for making that number..

But if you were particularly interested in true automatic number deletion, there is always 1^N = 1:

I also never played around with 0, negative numbers, or things like this:

But there are certainly similar feedbacks you could do with 0 to delete numbers via multiplication.

Limit Testing

I only ever bumped into the integer limit by accident, but there may be practical uses for it. Any sufficiently large output is replaced by 2147483647, which is 2³¹ – 1.

In the negative direction, you get -2147483648, which checks out, as twos complement will traditionally have a minimum value one smaller than the negative of the maximum value:

Division by 0 is apparently fine and dandy, and will output 0 as the quotient and the dividing number as the remainder:

If the division has no remainder, it won’t bother to make a 0 (even with space for it).

In any other case, the remainder has to be put onto a belt and carried away, otherwise the component clogs up. A component can only hold 4 values in each input, and 2 values in each output. If it has to hold more than that, it will refuse to act. Maybe that’s why the steam reviewer wanted to delete numbers. By not getting rid of the remainder 28 here, I can’t get any more of my definitely-numerically-sound 6083523s:

Is there More?

One must wonder if at some point, maybe every target number is just 2147483647, and Beltmatic goes from being varied to being very very easy. I found conjectures on the steam forums that this may be the case, but nobody has claimed to get that far from a cursory glance. For the sake of experimentation, I did upgrade my exponentiator one tier further, to see if the next number was massively larger than the 3 million I already had to make:

It was not. My 2% increase in exponentiation speed was accompanied by a 1% increase in the amount of values to deliver, and a 4% increase in the new target value. It’s a long grueling journey to get to the integer limit, if it ever happens at all.

For the curious, here are the machines that built the 17592:

The 79233:

And the 3063744:

Ultimately, I think that Beltmatic has pretty limited replay value, but for the 10 or so hours I spent playing, and then just as many hours making this blog post, I really enjoyed it. I even had Beltmatic dreams. I just never really felt like it was beneficial to build something like the super cute factory in the loading screen:

I’m sure that Beltmatic aesthetics optimization could be a fun endeavor. Someday, if I end up playing it again.

Edit: the RNG

After posting this, I couldn’t get the idea of the pseudorandom number generator out of my head. I had a horrible night of sleep wondering about 2s and 4s and feedback loops. I designed this almost completely in my head, and when I woke up I built it:

This will generate a random number between 0 and 65535, every second. At the moment, it’s definitely mostly a 65535 generator, because the feedback belt is very heavy on the 4s. In a more representative steady state though, after days and days have passed, the big loop highlighted in red will have a high entropy mix of 2s and 4s:

In the process of designing this, I also realized how to use the divider as a replicator. I multiply a value by 7, then divide by 6. I get the same number out as the quotient, but I get a copy of that number as the remainder. This is how I clone my signal to do logic gates. The logic gates themselves are using 4 and 2 as binary 0 and 1, and the following facts:

• (2 + 6) × 2 – 6 = 10 = 1 × 6 + 4
• (4 + 6) × 2 – 6 = 14 = 2 × 6 + 2
• (2 + 6) × 4 – 6 = 26 = 4 × 6 + 2
• (4 + 6) × 4 – 6 = 34 = 5 × 6 + 4

The right side value, the remainder, gets placed back on the belt, so when the belt has 22 or 44, it creates a 4. When the belt has 24 or 42, it creates a 2. I specifically cleared a single value from the belt at 8 key places so that it would be reading adjacent values instead of the two copies of the same value. This leads to a very inefficient random number generator, like I have done before in Opus Magnum. It’s inefficient because while it does cycle through some 2²⁰⁰ish different states before looping, it doesn’t really do so “randomly”, and when only sampling 16 bits the result is prone to huge streaks of the same number, like 65535 here.

The quotient, 1, 2, 4, or 5, is multiplied by 4 and divided again by 6, with the remainder going into an adder with itself to eventually become 2147483647 + N = 2147483647, another form of number deletion a little more degenerate than 1^N = 1. The quotient is now 0, 1, 2, or 3. Combining 8 of these into a base 4 value, it can theoretically express anything between 0 and 65535 with equal likelihood.

There were several awkward setups for this. Getting the feedback loop populated with a bunch of values, but not all 4s as that gets stuck into a loop of making 4s forever, meant I brought in a 2 extractor briefly. Clearing values so that things lined up how I wanted them was error-prone. I’m still not sure it is exactly what I want it to be, but I’ll leave it running for a day or so and check back in. In theory, it should produce any given value once per 18.2 hours, so I might see 1/16.5k on my level progress by tomorrow.