Making a computer in Opus Magnum

I mentioned in my previous post about Opus Magnum that people have built computers in game. I am one of those people, for an appropriate definition of computer. Let’s take a look at what, how and why, and see some more excellent gifs!

Note: this post will assume that you know what Opus Magnum is. If you don’t, feel free to read the beginning of the previous post for a quick crash course in the game.

Opus Magnum Tournaments

I didn’t build a computer in Opus Magnum simply to prove it could be done. No, this was for a competition, and the structure of that competition is relevant to the story. So let’s first talk about Opus Magnum tournaments.

2019

The first tournament was in early 2019, led by RP0. He stirred up a fair amount of interest from top players on Discord and reddit, created several custom puzzles in the editor, and put together a small amount of infrastructure to collect and compare solutions. When it began, every player was shown the first puzzle. We had a week to send in solutions for “Unwinding.”

Unwinding, the original Opus Magnum tournament puzzle — Humble beginnings, rearranging iron to form a stick

Solutions were made in secret, and we could pick between any of four goals. Goals included some primary metric, like cycles, that you had to try to minimize, but also secondary metrics to define how ties were broken. People could talk about the puzzle, but nobody could know anyone else’s solutions or scores until the deadline when everything was revealed.

Scoring

Everyone who submitted solutions earned some number of points for each, with the winners of each metric getting 10 points. Add the points to a running total to see who is in the lead after each week. The prize for winning a week, or even the entire tournament, was only bragging rights. But regardless of reward, I always found it fun to work on a problem, then see how others approached it.

For Unwinding, I had the best solution for “cycles, with ties broken by area” using the solution below:

Unwinding in record cycle count — One of my solutions to Unwinding, and the only one of my solutions to win a metric (cycles primary, area secondary)

As a side note: the community was still trying to streamline the competitive process during the 2019 tournament, so the number of separate metrics, as well as the number of solutions a player can submit, vary throughout this post.

A Special Final Challenge

The weeks of the 2019 tournament went on, and the puzzles got harder. But the real treat came during the final week of the tournament. Instead of one puzzle, we were given 5 puzzles. But not independent of each other, since the puzzles were very similar..

We had to make a single machine which solved all 5 puzzles.

Wheel Inversion, the week 10 puzzle from the original opus magnum tournament, but it is not as simple as it looks — One of the 5 variants of Wheel Inversion, the final puzzle of the 2019 tournament. In other variants, the 7 atom input had its 6 outer atoms changed to other combinations of the cardinal elements and salt. For every variant, the output wheel could be reached from the input by performing the set of replacements on the right.

The 5 different versions of the puzzle all used different wheel inputs and outputs. They each had gold in the center, and some collection of earth, fire, air, water, and salt around the ring. For every puzzle, the output could be reached from the input by replacing earth by air, fire by water, air by earth, water by fire, and leaving salt as salt.

Solving Many as One

This may seem like a very peculiar challenge. But what RP0 provided with this final set of puzzles, is the first “computation puzzle” in Opus Magnum tournament history.

What I mean when I call it a computation puzzle, is that the input and output are related algorithmically. In order for your solution to successfully invert the colors of an arbitrary wheel, you can’t do normal Opus Magnum things. You can’t get away with grabbing a bunch of water inputs and sticking them onto the gold atom, and counting that as done. That solves one of the puzzles but not all of them. You also can’t get away with spinning the input around 180 degrees. That solves one of the puzzles (the one in the image above), but not all of them.

To solve all of the puzzles, you needed to have some logic inside of your machine.

Solutions

To finish out the history lesson here, I will share two gifs of solutions to this puzzle. But know that the story is only just beginning.

One problem with solving many as one, is that the usual method of displaying a solution as a gif can be inadequate. So while the solution below clearly solves the puzzle it has been given, you need to look more closely to see how. One at a time, it removes atoms from the input. It then passes them through some gauntlet of single atom inputs, outputs and arms. Out the other side, comes a new atom. And wouldn’t you know it, that new atom is the “inverse” of the atom that went in, every time.

A solution I made for Wheel Inversion, which solves all variants — Wheel Inversion, sum optimized, shown on one of the variants. The atoms are inverted one at a time, by testing which outputs will consume them.

The above solution was made by me. Another solution to this puzzle, made by PentaPig, is shown below. He decided to present the multiple variants by showing them all in one screen. This visual is especially awesome because it shows where sequences diverge from one another depending on the input. Although, note that the 5 variants shown below are not the 5 test cases given by RP0, and they only invert one of the 6 atoms in the wheel. PentaPig’s full solution runs 6 times as long. He was kind enough to make the recording below as a demonstration of what happens when his solution encounters each type of atom.

A cost optimized algorithm made by PentaPig, shown on 5 example wheels that only require inverting a single atom. His solution to wheel inversion used this algorithm but inverted all 6 atoms of the actual variants. The version here is chosen for presentation instead of the longer one, which had 50g and nearly 20,000 cycles.

The 2021 Tournament

Consider all of the above an appetizer, and don’t worry if it leaves you with lots of questions. I said I built a computer. You have to squint really hard to believe me from the wheel inversions above. Fortunately, the story of this blog post takes place in 2021, not 2019. The 2021 tournament was more polished, had some powerful players, and ended with something incredible.

Meet the Players

Leading the tournament going into the final week was Rolamni. Rolamni had not participated in the 2019 tournament. He got a single week victory in 2020 but ended in 4th overall. However, he had clearly emerged as a 2021 favorite with back to back wins on several very hard puzzles.

Second in the standings was PentaPig, the author of the second Wheel Inversion gif above and the overall winner of the 2020 tournament.

Third was jinyou, author of several of the best known solutions to the campaign puzzles and consistent tournament finisher.

And in fourth, was me. I had won overall in 2019 and been the host in 2020, so I was technically undefeated, but I needed to do a big leap here to keep that up.

The 4 of us had a lot of distance from the rest of the field. Of the nearly 70 entrants, we finished consistently at the top and there was no realistic chance that anyone else could take the crown with only one more week of points to go.

The Puzzle

Our 2021 host, brookieoz, was eager to keep up what had now become a tradition. The tournament must end with a computation puzzle. The final week announcement came.

Your solution must implement subtraction of 8 bit numbers. In Opus Magnum.

There was an entire document on the specifics, but suffice to say that fire is 1, salt is 0, and the example puzzle is the image below. Input 1 encodes 22 in binary (00010110), input 2 encodes 19 (00010011), and the output encodes 22 – 19 = 3 (00000011).

Now our Opus Magnum computation puzzle is an actual computation — One version of Explosive Logic Unit, the final puzzle in 2021. Long sticks encode 8 bit numbers, fire as 1 and salt as 0. For every version, the output is equal to top input minus second input, in binary two’s complement.

There were extra inputs, salt bonded to fire, to use however you please. These would never change. But the 8-atom inputs, call them A and B, could in theory be any sticks of salt and fire. For every instance of the puzzle, the output would be binary for A – B. And your machine needs to get that answer, no matter the inputs.

How?

Well, when trying to mimic a computer, a good place to start is with learning how a computer works.

What is Your Computer Doing

Whatever you are reading this blog post on, be it a desktop computer, phone, smart fridge, it has a processor. A processor is a small electronic machine with a protocol for how its inputs relate to its outputs. Rather than “know” anything, a processor has arranged metal and semiconductors in the right places. When binary-coded values, memory addresses and instruction codes land on its input ports, the output ports get the correct voltages.

Built on top of these processors are operating systems, interfaces, tons of accessories to make the results usable. But at a processor level, the only things that change between browsing the internet, playing a game, or writing code, are the inputs.

Logic gates

The starting point for understanding most modern computers is combinational logic, using basic building blocks called gates. Given some signals which encode either 0s or 1s, gates manipulate them to make other 0s and 1s. Every logic gate has a representation as a truth table, like below.

Logisim is a good program — The truth table (top) and Logisim depiction (bottom) of an AND gate

Assuming you have access to a small toolbox of gates, and can copy signals to use in multiple places, it is possible to build up to some very complex logic. Here is addition of two two-bit numbers using just AND, OR and NOT.

Not a particularly friendly one, mind you, but a good one — The truth table and Logisim depiction of a 2-bit adder. The AND gate is as shown in the previous image. Pointed 2-input gates are OR, and the single input triangle is NOT. This same logic could be scaled up to create an 8 bit subtractor, like is needed in the puzzle, although it would be a very large circuit

So if we can build logic gates in Opus Magnum, we can probably make a solution to the challenge, eventually.

Logic gates in Opus Magnum

AND

Opus Magnum doesn’t come equipped with logic gates the same way that the Logisim program above does. So we have to reach the same truth tables using arms, glyphs, and instructions. Specifically, assume we would like to build an AND gate. Start with two unknown atoms as inputs, they could be fire or they could be salt. After some set of instructions, we should be able to put a fire on the output if both inputs are fire, and a salt otherwise.

Each machine is doing the same thing, but when considering differences in input you achieve computation — The AND gate using fire/salt to encode 1 and 0. The 4 rows of the truth table are shown here from left to right, and the output at the bottom is correct in all 4 cases

Well, that’s both really cool, and slightly horrifying. It works, but it takes a fair bit of space and glyphs and it produces waste. It works by putting both unknown atoms on the “triplex bonder”, which is a special glyph only able to work on fire atoms. When the two atoms are both fire, the triplex bonder connects them, so that a subsequent rotation can move one of them to a place only reached in the two-fire case. Otherwise, one atom (be it fire or salt) stays on the triplex bonder. By passing it over a calcifier, we can guarantee that it becomes salt, and the two branches converge once again on the output.

One feature of this sort of branched execution, is the handling of “ghost atoms.” Arms grabbing at nothing, which exist to handle the case that something is there. For simple examples, I find it really cool to watch these gifs overlain with each other, so that the ghosts exist.

This gif was actually a pain in the ass to generate — The 4 options overlain using transparency, showing all the “ghosts” that a machine must handle when conditions branch in their behavior

OR

Another useful glyph in the game is duplication. Duplication will turn salt into one of the cardinal elements (which includes fire) if the cardinal is present. Duplication allows for a very easy OR gate, although still producing waste.

Why must the classic logic gates be wasteful? — The 4 rows of the truth table for a 2-input OR gate, which uses the glyph of duplication

NOT

The last piece of the logic diagram above is a NOT gate, which turns fire into salt and vice versa. This is actually the hardest in the set, because you need a known fire present. Fortunately, the salt-fire inputs exist to give a guaranteed fire. The rest of the operation can use triplex, calcification, and duplication as before.

Not going to make a transparent overlay for this one, sorry — One implementation of a NOT gate, which uses an extra salt+fire input to provide a means to test and duplicate fire atoms

Is This Good Enough?

In theory, this is good enough. You can write out the combinational logic circuit for 8 bit subtraction, convert each gate into the game elements above, and join all the ends to each other. You would also need to begin by putting some guaranteed fires into every NOT station, because you only have two sources for those inputs. The result would make a large amount of waste, take a lot of space and cost, and be a pain to lay out and program.

But it would be enough, at least for a solution.

Remember though, that this is a tournament. Solutions become scores. Here, there was only one metric, and it was cost/5 + cycles + area. A weighted sum of all main metrics, to force you to consider all three. By the metric, I would say that the solution we have blueprinted so far is not looking very good. But we can do much, much better.

Theory Models of Computation

Even though combinational logic is the most efficient way we know of, to get computation out of metal and semiconductors, it is not the only way to compute. There are other models of computation. Some of them translate much more effectively to Opus Magnum.

The model that we are going to look at is the Finite State Machine.

Finite State Machine

A finite state machine is basically a glorified flowchart. Bubbles are “states” and arrows are “transitions.” To progress, read the input one symbol at a time, and follow the appropriate transition to the next state. If you reach an “accepting” state before running out of input, your input is accepted, otherwise it is rejected. Shown below is a finite state machine to answer the question “does the input have a 000 in it.”

MS Paint is valid — An example Finite State Machine. Beginning in the left state, read an input of 0s and 1s one symbol at a time and follow the arrow for the symbol read. Reaching the rightmost state means the input is accepted, which for this machine happens whenever there is a 000 in the input

You can do more complicated things than answering yes/no questions. To implement binary subtraction, we want a finite state machine that can add to some output depending on the state it is in. Technically this concept is a finite state transducer. But, I’ll continue to call it a finite state machine. The only difference is that now states include an optional “Write” command inside them.

The Algorithm

What does a finite state machine for binary subtraction look like? Well, let’s do some binary subtraction by hand and pay attention to what we are doing at each step.

35 minus 26, in case you needed alt text to tell you that

This is going to be exactly like base 10 subtraction, but with 10 – 1 = 1. So we start with the rightmost bit. 1 – 0 = 1.

We can teach a computer to do our algorithm if we understand it

Next we do the bit to its left. 1 – 1 = 0, another easy one. Left of that is 0 – 0 = 0, yet another easy one.

Still easy to understand this computation

Next is where it finally becomes tricky. 0 – 1 is negative, so we need to “borrow” from the next bit over. When borrowing, we treat the 0 as a 10, and write the -1 to offset it on the next column over. 10 – 1 is 1, so we write a 1 in the bottom.

Now we have the same situation, but with a borrow already present. We have two different -1s to handle, one from the bottom number, and one from the existing borrow. So if we treat the 0 as a 10, we have 10 – 1 – 1 = 0. Write a 0 on the bottom and borrow again.

Since we have reached 0s from here to the left we are done, the answer is 1001 aka 9

And now we have 1 – 0 with a borrow, which is 0 and completes the subtraction.

The State Machine

Let’s reflect on what just happened. We read our inputs from right to left, first the top input and then the bottom. We always wrote something after we read one symbol of each input, and before moving to the next bit. And we did something with borrows, whenever we needed to, that changed what we wrote and what our next steps were.

So the state machine would look something like this.

A finite state machine for the continuous part of binary subtraction — The process which we followed to do the subtraction by hand. Each read step takes the next bit reading from right to left. Arrows in red and green happen automatically after writing a value

Convince yourself that this matches what we did when subtracting by hand, and then convince yourself that it can further be simplified, because some of the states above the borrow/no borrow line are identical to states below it.

It's almost too easy — This is the same algorithm, but a simpler state machine. States that do the exact same thing can always be combined, which applies to 3 pairs of states in the earlier machine

I used this state machine to implement binary subtraction. 4 hours after the puzzle was revealed, I had written down some scratchwork equivalent to the diagram above. I had the rest of the time, to work on implementing it.

Translation Back to Opus Magnum

I’ve suggested that a finite state machine translates nicely to Opus Magnum. It’s time to demonstrate how that is true. The main concept is that your “state” is some configuration of atoms on the board. Every transition will attempt to modify the state by interacting with the next important input atom. As long as you can agree what configurations refer to which states, and make sure that all the transitions end up exactly where they should, then you have implemented the finite state machine.

Conditional Movements

I initially envisioned my important stateful atomic blob as a large rotating object, bonding things here, breaking them off there, doing who knows what to keep the states aligned. But after a little bit of experimenting in game, I made the requirements more concrete.

Opus Magnum computation mechanics, now with an algorithm in mind — A test atom on the triplex bonder will move the fire molecule if the test atom is fire, and do nothing if not. This allows a different state transition for 0 and 1

Consider the two fire atoms shown as belonging to some larger structure. The solution wants to place an unknown atom on the triplex bonder, move it as the arrow shows, and conditionally move the structure by one tile. Afterward, your test atom is guaranteed to not be bonded to the structure. Either it was fire, so it moved the structure and then unbonded, or it was salt so it never bonded in the first place.

There are two fire atoms, to provide a difference between the “borrow” and “no borrow” state. If the left fire atom is on the triplex, we are in the no borrow state, and if the right fire atom is on the triplex we are in the borrow state.

After moving one test atom, we naturally have fallen into the 3 middle, unlabeled states. You can verify that no borrow and 0, ends up in the same place as borrow and 1, while the other options are distinct. A lot of good work for only two atoms.

Symmetric Action

Our 3 states are now separated by 2 tiles of motion. Notice in the state machine diagram that 0s for the next step always go up-right, and 1s for the next step always go down-right. We can keep getting away with single-tile translations. In fact, we can make our structure a single fire atom wider, and just do a conditional move in the other direction.

Plus, symmetry is pretty — Conditionally moving the stick right, and then left, turns two starting states into 4, exactly like the diagram

You can step through each of the possibilities, and see that this indeed will get you to the proper states on the right side of the diagram. The important cases where there are alternate paths to get to the same state, all converge perfectly.

Writing 0 or 1

Writing seems like the hard part. We have a stick of fire, how can we identify which of the 4 positions it is in?

There is an elegant answer to this as well! Use the glyph of duplication, and extend the stick to contain a pattern of alternating fire and salt. Depending on which one rests on top of the glyph of duplication, you can read a 0 or a 1.

Opus Magnum is just powerful enough to make this computation easy — To write the proper 0 or 1, we duplicate from the stick itself onto a known salt atom

Closing the Loop

Finally, there are the red and green arrows to get you from writing an output, all the way back to the borrow/no borrow states.

If you follow the 0s, you can see that two of those arrows don’t require moving at all. 0s leave the stick in the same place, because salt doesn’t bond on the triplex bonder. It’s only the leftmost and rightmost positions of the stick, that need to be brought one tile back toward the center before we check the next input. And here we use the idea of ghost atoms.

Yes this is another MS Paint edit — Borrow, 0, 1, write 0, leaves us in this position. That is the only way an atom ends up on the circled tile, so grabbing (or bonding) there will isolate that state from the flowchart

There is exactly one tile, where a stick in the leftmost position leaves an atom, and no other position does. It’s the left atom of the stick in the leftmost position, and we can try to grab it. Or bond to it. In either case, we gain control of the stick only in the leftmost position, which we are trying to move to the right. Likewise, there is one tile on the right with the same property, for when we are trying to move to the left. You can attempt both at once without crashing, knowing that they cannot be simultaneously true.

Long stick, the pinnacle of computational power — No Borrow, 1, 0, write 1, leaves us in this position. That is the only way an atom ends up on the circled tile, just as above. Note also, the stick in the image can be shortened as it is below in the finished solution

I made some solutions with grabs on those two tiles, but grabbing is slow. This algorithm could move very fast, and it is better to move the stick by bonding to it. That gives a little bit of character to the resulting solution, since it has arms that look like they are partying, moving salt back and forth in a mostly useless way.

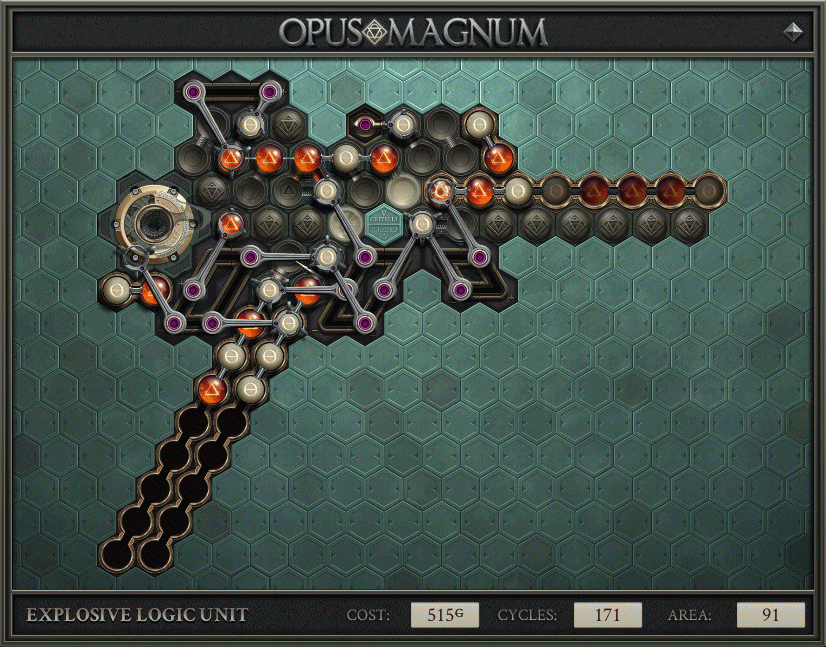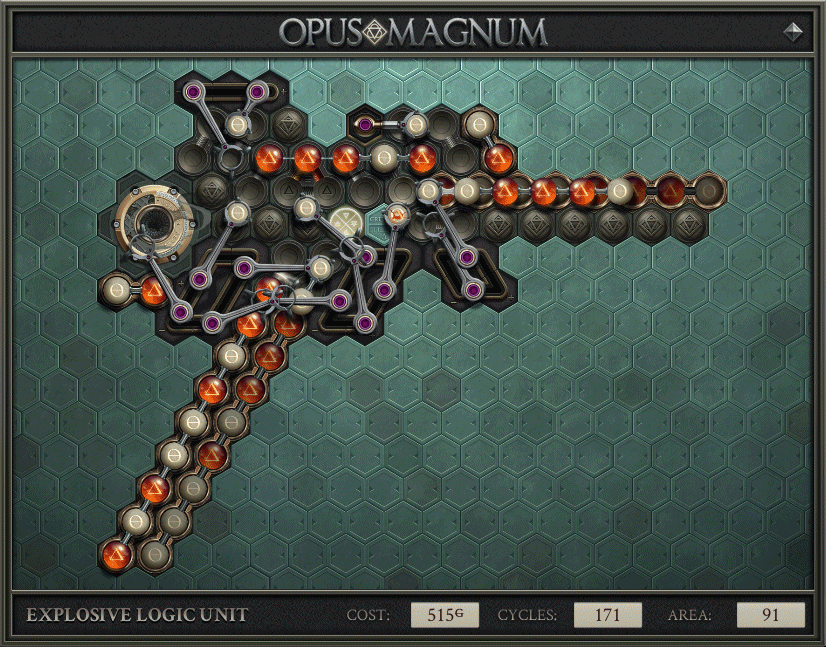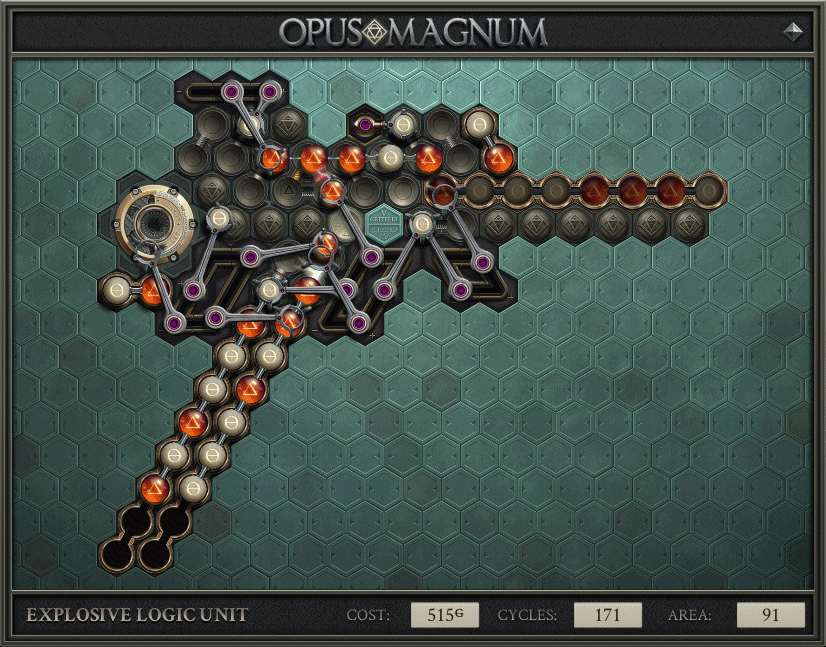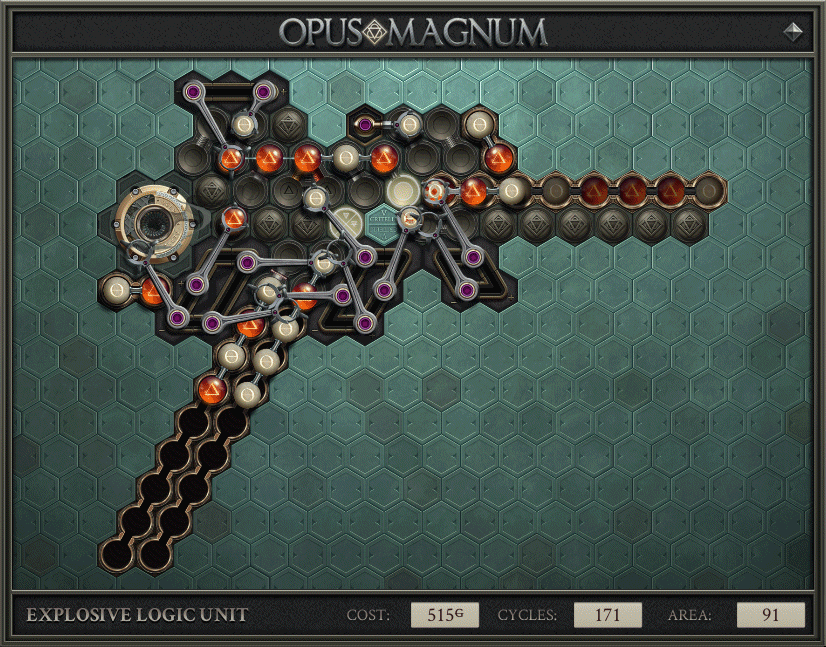
My Solution

The finished solution, on a test case of -91 – 23 = -114 (equivalently, 165 – 23 = 142), which is a test case that happens to visit every state in the state machine. The loop consists of “build stick, make 6 outputs, destroy stick.” The statistics of 171 cycles / 91 area, are taken after the 6th output, before destroying the stick. The metric score of this solution is 365, coming from 515/5 + 171 + 91

All of the important ideas come from the section above, but there were still some i’s to dot and t’s to cross. Minimizing the big stick down to 5 atoms (emptiness is the same as salt when it comes to duplicating). Processing 8 pairs of input atoms and then resetting to “no borrow” before reading the next inputs. Efficiently generating the stick by arms that have a use in steady state. Also, plain old Opus Magnum difficulty. Programming track loops. Making sure that there were atoms where I needed them, without slowing down the machine.

I made good use of the provided time. It took a few iterations to end up with the solution above, and I made this imgur album to describe the journey. Prior to this blog post, the album was the most complete explanation of how this solution worked.

But, yeah, looking at this machine I felt pretty confident. It would take a miracle to beat me, and I felt more like my solution was the miracle that would beat others. The score by the metric come out to 515/5 + 171 + 91 = 365 metric points. I had no guesses how the best logic gates/truth table solutions would score, but I was confident they had to be more complicated than this.

The Waiting Game

I was pretty obnoxious in between making this solution, and the reveal.

Sometimes you just know you're sitting on something remarkable — Thank you everyone for putting up with me

Fortunately, there were other ways to pass the time. One community member going by “panic” had built a tool to validate the solution files against the entire collection of 65536 input molecules. In glorious aesthetic fashion, he displayed the space as a hexagon of pixels. Red is fail, white is pass, and the lines across each hexagon axis corresponded to constant input 1, constant input 2, and constant output.

We unit test our Opus Magnum computers — The hexagon is 65536 pixels large, and every pixel is drawn by generating a new version of the puzzle with different inputs, running your solution on it, and checking whether it completes. Thanks to panic’s effort, this can run in seconds on my solution and prove it is correct for every test case

This tool evolved into omsim, a fast and generic solution file validator for Opus Magnum. But in its infancy, as a scorecard display, I had a lot of fun with it. I made solutions that failed only for specific test cases, and made the highest effort April Fool’s post I had made in a long time. Many people were sharing their sierpinski triangle scorecards, which seemed to come from an error in truth table solutions. The whole atmosphere in discord was amazing as the dozens of competitors kept their solutions a secret, but all were clearly focused on this incredible puzzle. Then finally, it was time for the reveal.

The Conclusion

Across 5 hours and two massive youtube videos, the reveal stream lives forever on the internet. You can watch it in full display and appreciate all 36 submissions, at the link here. The big names ahead of me in the tournament all finished pretty well. Rolamni in 7th with 580 metric points. jinyou in 6th with 560. Pentapig in 4th with 515. Almost everyone was using truth tables (besides Steven whose submission implemented a well known dumb programming language for memes. I wasn’t joking when I called the guy out in my previous Opus Magnum post.)

3rd place went to panic, who made the best truth table solution at 497.

The 3rd place solution by panic, who had the best result of anyone to use a truth-table based solution. 770/5 + 215 + 128 = 497. The limiting feature of truth table solutions is the borrow bit, which must be passed as a physical object. I won’t be fully explaining how this solution works

2nd place went to Voidify, the only other person in the field to have recognized the power of the finite state machine. Their writeup indicates that they arrived at the same conclusion, but using a different paradigm of a “register”, which makes a lot of sense in this case. However, a difference in converting to a layout, left them with a score of 452. A decent nosedive in points vs 3rd place. But few were prepared for how much lower it went.

My solution makes its debut in the tournament standings, in first place!

Shown above is the timestamp where my solution arrived on stream. There is commentary from brookieoz and myself who already knew it was coming, but additionally from mr_puzzel, whose reaction is genuine and wonderful.

I ended up winning by a very large margin. I took 10 points and set a very harsh curve, such that PentaPig got 8.13, jinyou 7.56, and Rolamni 7.31. This difference shook up the order of the top 4. It was enough that I pulled off the overall tournament victory by less than one point over PentaPig in 2nd and Rolamni in 3rd.

My design was everything I was hoping for: cheap fast and small all at once, and lived up to the high expectations. I was thrilled, and proud. Reflecting on it now, 8 months later, I’m also excited for the next installment..

2022 Tournament

There will be another tournament in 2022! It is scheduled to begin the first week of the new year, hosted by Bist and coordinated using a website built by panic. Find more at http://events.critelli.technology/, where a “week negative one” already exists to familiarize players with the process.

Much like every optimization tactic discovered in the last 4 years, the cat’s out of the bag now regarding finite state machines. I only expect the 2022 tournament to be even more competitive. But don’t let that discourage entry – I look forward to seeing new names trying out the game. It’s a wonderful experience, learning by playing tournament puzzles alongside veteran players. Perhaps by the final week, you too can build a computer in Opus Magnum.