Matching Patterns using Opus Magnum
Hi all, and merry Christmas to those of you who celebrate it! Here’s a present from me, a long-awaited blog post about the computation puzzle from the 2023 Opus Magnum tournament. The previous post about that tournament can be found here. This post will complete what was left incomplete at that time. For more about each solution you can look at the results video here, and the spreadsheet here.
As is tradition, the final challenge of the tournament was a computation puzzle. Previous challenges have been to invert a wheel of cardinals, take a derivative, do binary subtraction, and simulate a well-known turing complete cellular automaton. This time, the challenge was string pattern matching.

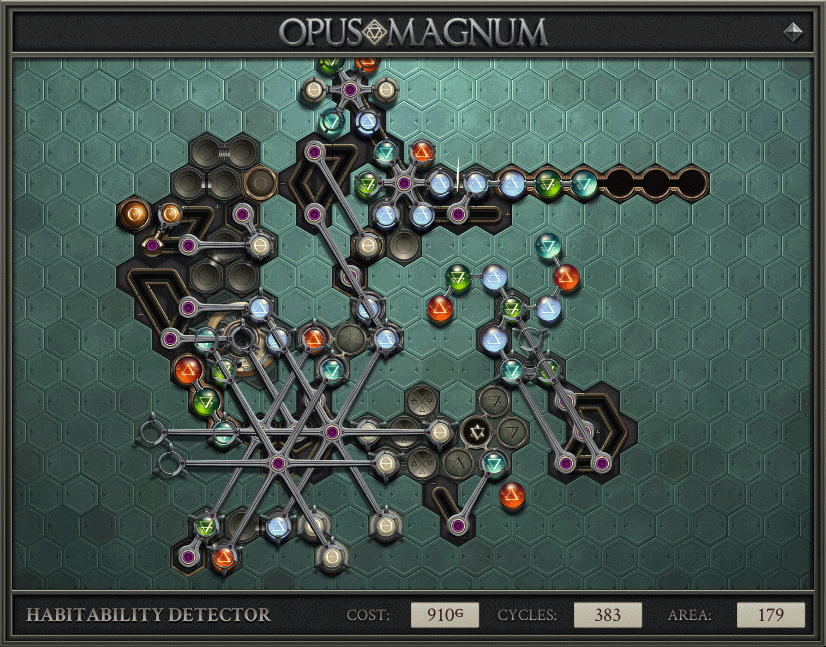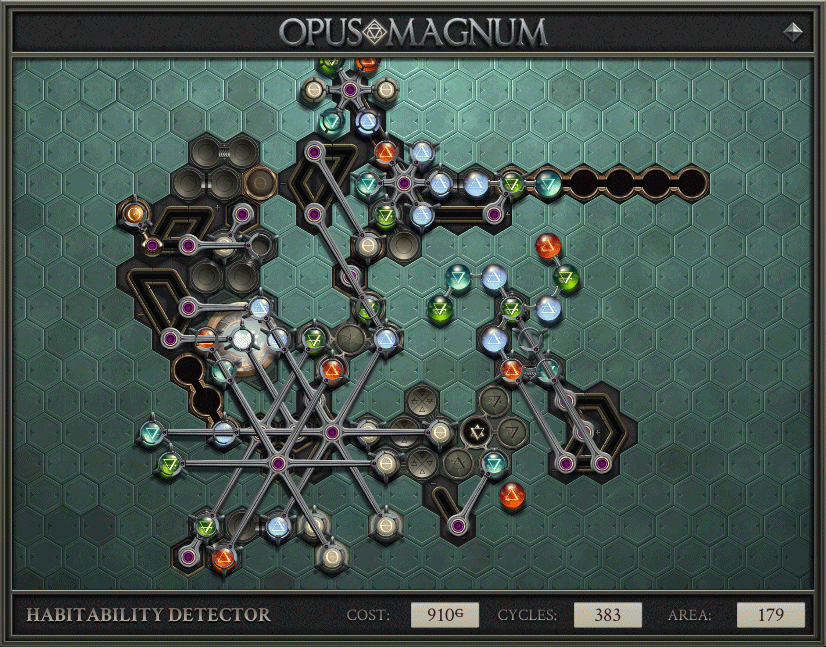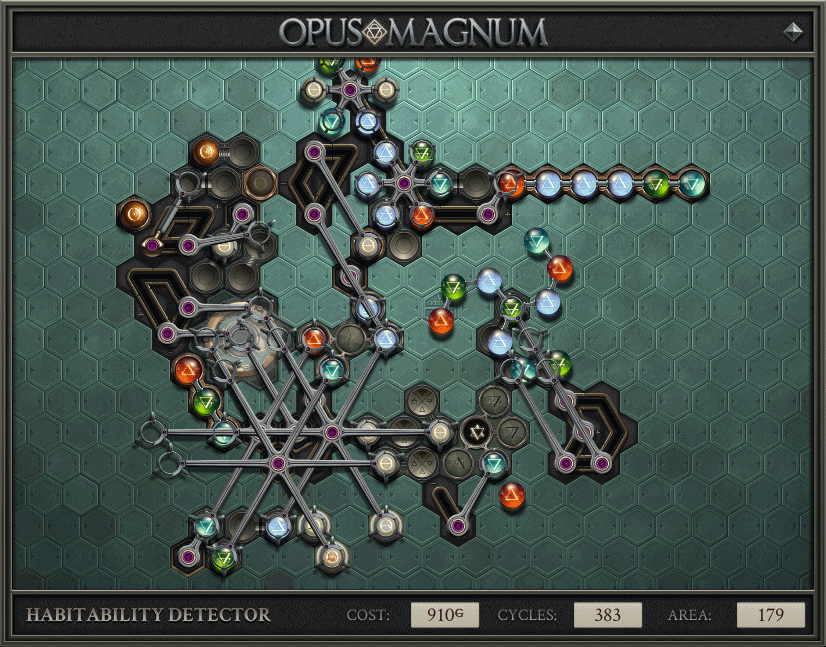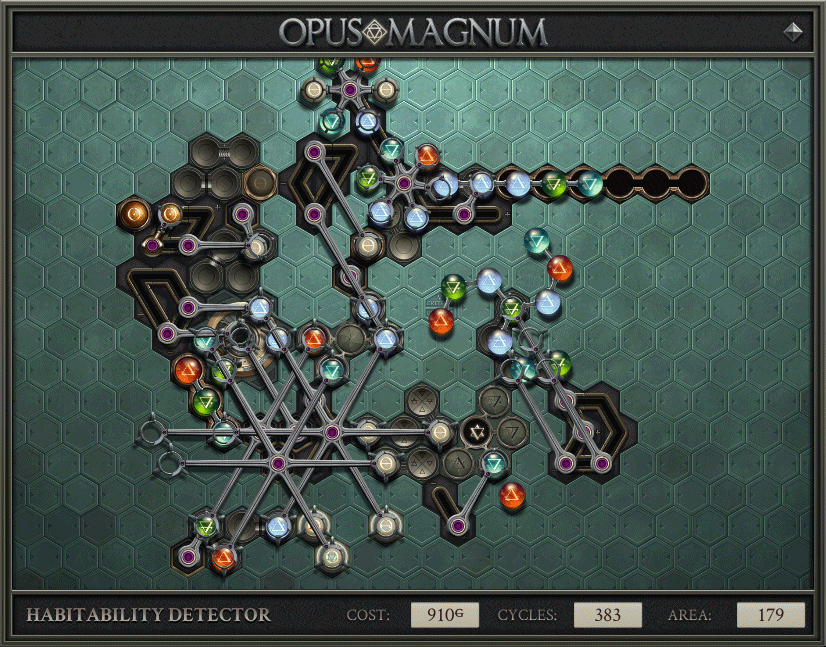
Meet the week 8 puzzle: Habitability Detector.
Understanding the question
In these sort of “presentations” like the image above, the puzzle designer lays out all of the allowable parts and tries to make them look nice. It’s meant to be eye catching, and only really informative to an informed reader. You can view the website for a full description, or just keep reading here.
The only output is a gold atom. There is a gold atom input. Why the heck do you need anything else?
Well, in standard computation puzzle fashion, your solution actually has to work for a much larger possibility space. The presentation only gives a single example. That atom of output may be gold, or it may be salt. The output should be treated as accepting any atom. Outputting the wrong atom for any instance of the puzzle is a fail condition, formalized by the validator contained in the submission website.
To understand whether we are supposed to output gold or salt, we must turn to information in the two sticks of elemental inputs. The gold/salt indicates a yes/no answer to a simple question: is the smaller pattern contained within the larger?
Lore
Within the story accompanying this tournament, pattern matching made sense. The main characters were analyzing samples recovered from all of the candidate worlds, trying to find any that were suitable for life. The samples were 6 atom long sticks. You had to handle each with care, using it only once to determine the correct output. The next sample taken from the input had no guarantees to be the same as the previous. Fortunately, the atoms in these sticks were guaranteed to be either fire, air, earth, or water. No metals, just the 4 cardinal elements.
In hand, the characters had their “match pattern”. 3 atoms, designating what needed to exist on the other world for it to sustain life. The example image shows air, air earth as the match pattern. In a crude sense, that seems to suggest a search for a planet with solid earth, and an atmosphere. Your machine needed to work no matter what the match pattern was, but you were free to assume it would be the same every time (so you could use as many of this input as you wanted when evaluating one sample).
Now, whereas all previous tournament computation puzzles had informationally-complex outputs, the output here was as simple as it gets. If somewhere in the sample there were the 3 atoms exactly as they appear in the match pattern, output gold. If not, output salt. And as previously mentioned, for the sake of the main characters, you had to get the right answer every time, with no guessing.
Warmup puzzle
Key to being able to find matching substrings, was the ability to find individual matches. That already is rather complex in Opus Magnum. If I am holding two unknown cardinal atoms, what can I use to determine whether they are the same, or different?
For the 2023 Opus Magnum tournament, panic made a decision. As in previous years, solving the computation puzzle guaranteed 10 bonus points, in place of a second metric. But this time, you could also get those 10 bonus points by solving just the warmup puzzle. So, meet Elemental Comparator.

Rather than sticks of 3 or 6 atoms, the two unknown inputs here are single atoms. They can once again be any of fire, air, earth, or water. If they are the same atom, output gold. If they are different, output salt.
In this warmup puzzle, there were no metrics. Players were encouraged to solve this smaller problem first, and then try to apply it to the full Habitability Detector. If you succeeded and solved Habitability Detector, your solution would be eligible for the weighted sum metric, and you would score additional rank points beyond the 10 bonus points.
But how?
Let’s go through each glyph provided by the puzzle, and see what it can and cannot do.
The ordinary bonders and debonders are completely blind to any difference between the different cardinals. Bonders are wonderful for handling information contained in the presence or absence of an atom. But to get to that point, we need something that will actually distinguish the type of our input atoms.
The triplex bonder is a little more promising. It was a key player in the binary logic puzzles, where fire encoded 1. Triplex will always allow us to find matching fire atoms. Since we have access to the Van Berlo wheel, we can also generate a known fire and use it to filter out individual fire atoms. But once we have filtered out all the fire matches and no-matches, we still can’t use triplex to tell the difference between matching air, water and earth atoms, and non matching combinations thereof. So what else?
Calcification will reduce all cardinal atoms to the same salt. It destroys information, so that’s useless. Duplication allows us to make copies, but can’t actually distinguish the key information on its own. And disposal is absolutely not going to help us here either.
That leaves only the star of this puzzle: the quintessence glyphs.
Unification
The unification glyph will create a quintessence if and only if the 4 atoms on its input tiles are the 4 different cardinals.
Notice that the 4 symbols on each input tile represent the cardinals. If there is a cardinal present on any one of the inputs, the corresponding cardinal’s symbol gets dimmer for all 4. This visual update happens at the start of movement phase, so it happens slightly in advance of the actual cardinal landing on it. But, unification is definitely the right glyph for this job. It is made for testing cardinals.

Shown above are two copies of the same machine. One of them has air and earth as input, and the other has earth and water. In this design, I’ve made it so that fire and air always get placed on the left two tiles of unification. The unknown atoms go on the right two tiles.
What this means, is that whenever the unknown atoms are earth and water, there will be a new quintessence formed. This quintessence can then disperse using the dispersion glyph below it, and recover the original air and fire. Meanwhile, the earth and water have now “moved” from the unification to the dispersion.
On the left, since the unknown atoms were wrong, they move away into a new place (here, a waste stick). On the right, since they were correct, they appear on dispersion, rejoin, and output.
This example only serves as a “earth and water” detector. But it shows how, in principle, we can tell earth, air, and water apart from each other.
All combinations
For the 16 possible pairs of cardinals, we can list the ways to sense them. By “sense them”, I am referring to converting the information unique to that pair, into presence or absence of some atom on some tile. That then means that all of the remaining work like selecting between salt and gold output can happen on bonders.
Based on what we know so far, the list is as follows:
- Fire + Fire – triplex
- Fire + Air – unification with known Water and Earth
- Fire + Water – unification with known Air and Earth
- Fire + Earth – unification with known Air and Water
- Air + Fire – unification with known Water and Earth
- Air + Air – ?
- Air + Water – unification with known Fire and Earth
- Air + Earth – unification with known Fire and Water
- Water + Fire – unification with known Air and Earth
- Water + Air – unification with known Fire and Earth
- Water + Water – ?
- Water + Earth – unification with known Fire and Air
- Earth + Fire – unification with known Air and Water
- Earth + Air – unification with known Fire and Water
- Earth + Water – unification with known Fire and Air
- Earth + Earth – ?
We still haven’t come up with a way to tell Air + Air apart from Water + Water or Earth + Earth. But do we need to?
Pairs algorithm
In short, we do not. We will come back to this question later, when discussing other algorithms. But you can absolutely solve the puzzle without being able to tell the various matches apart from each other. All 4 of the matching pairs need to result in the same thing – a gold atom being output. As long as you can split the space of all combinations into those where there was some match, and those where there was not a match, you’re golden.
Using this same insight, we don’t need to actually figure out whether unification was successful after each attempt. We can just try every possible combination one after the other, and check at the end whether any matched. That gives us the premise of the “pairs” algorithm. Put each pair of different cardinals on unification glyph along with the two unknowns. Quintessence is formed if and only if the unknown atoms are not a match.
How do you test all pairs? The easiest way is using the salt input and Van Berlo’s wheel. Shown below is a machine that cycles the berlo through Fire, Air, Water, Earth, Fire, Water, Air, Earth. Within this sequence of 8 atoms, you test every pair at least once. We referred to this as a “Gray code”, due to the principle of using as few changes as possible to advance to the next test, shared with binary Gray codes.

Nice features
The pairs algorithm is very simple. It systematically singles out each possible no-match, which lets it answer the match/no-match question on a single unification glyph without high expense. It uses the Van Berlo wheel and the salt input, both of which you can only place once, making it hard to run many times in parallel, but it uses them well.
If all you were solving was Elemental Comparator, you might wire up a couple bonders to select the salt or gold output, dispose your waste, and then call it a day. For completeness, here is a pairs algorithm solution to Elemental Comparator, cloned 16 times to represent all 16 possible test cases. The selection between salt and gold is done by pushing quintessence whenever it is formed, onto a bonded stick containing both. Whichever atom ends up in the gripper is the correct one to output.

This is achieving an output every 30 cycles, where 24 of those cycles are used to perform the 8 comparisons, and 6 of them are downtime to get rid of waste and prepare the next pair of test atoms.
With that in mind, it’s worth thinking about just how many comparisons it takes to solve the full Habitability Detector.
Naïve answer: 72
We need to process 6 independent samples to complete the puzzle. There are 6 atoms in each sample, and 3 in the match pattern. The match pattern can appear in one of 4 places. It can be atoms 123, 234, 345, or 456. If it is none of these, then the sample does not match. It seems then, like we might need to make 12 comparisons to evaluate one sample, and 72 in total.
notgreat made a pretty understandable pairs solution that performs 72 comparisons, at 24 cycles per comparison. That is shown below, first on a matching substring input and then on a non-matching one.
The score for any solution is “cost/5 + cycles + area”, lower better. notgreat’s cycle count is bounded below by 24 × 72 = 1728. The contribution from extra latency, cost and area is very minimal. Submitters who used this approach, namely notgreat, Genius42, and Topomouse, ended up with a score near 2000. Score was heavily determined by cycle count, which in turn was heavily determined by algorithm.
Using a better algorithm
A better algorithm can mean either of two things. It can mean a better algorithm for breaking the string pattern matching problem down into individual comparisons, or it can mean a better algorithm for performing those comparisons. We will look first at the former.
We don’t always need 12 comparisons to make an output. If we find a match in 123, we know the output is gold and there’s no reason to check any of the rest. Similarly, within a set of 3, as soon as you find a no match you should move on to the next set without finishing it. With this sort of “short circuit” evaluation, we might be able to solve the puzzle in fewer comparisons per sample.
However, two things get in the way. One is that opus magnum has a fixed instruction tape, so all of the logic behind short circuits is complex. As for the other: For better or worse, panic made the call to grade our solutions on their worst case performance.
Specifically, the validator on the website would run 4⁹ = 262144 test cases covering all valid inputs. It would compute the weighted sum of each, then show the worst number from any test case. Accordingly, there is no benefit to having better average or best cases. We need a better worst case.
Better worst case
If you look up efficient string pattern matching, you will find the KMP algorithm, named after Knuth, Morris, and Pratt. The KMP algorithm provides a better worst case number of comparisons needed to find matches within a string.
To understand KMP, try to come up with a pair of inputs where short circuits still give you the worst case. You’ll end up with something like the below:

It turns out that atoms 1 and 2 of the match pattern must match each other, for this worst case to occur. Accordingly, you can improve things if you first compare atoms 1 and 2 of the match pattern against each other. This only has to be done once ever, since the match pattern never changes.
If we know they match, then any atom that matched M2, doesn’t need to be compared against M1. It’s already known to match, saving us 3 comparisons on our worst case.

But you may be worried that a new worst case comes in to replace this one. It turns out, no. All other cases are guaranteed to have enough short circuits somewhere.

This is the essence of the KMP algorithm.
KMP in practice
Due to the complexities of fixed instruction tapes, a good KMP build would hard code everything to the new worst case. For KMP, that worst case is now 9 per sample. So, performing 1 comparison at the very beginning to learn about the match pattern, and then 9 comparisons per sample, totals to 55. The solution would also need some complicated logic to deduce the relevant short circuits.
This is possible, as demonstrated in the solution below by Bambi. Shown are a passing instance, a worst case failing instance with M1= M2, and a worst case failing instance with M1 ≠ M2.
This is a tremendously complicated solution. The quintessence in the bottom center holds the result of the first comparison between the atoms of the match pattern. It is present only on the 3rd of the 3 videos above, and modifies control flow appropriately.
The unknown atoms are duplicated onto salts, which allow the machine to read from dynamic positions within the string. This gives a lot of flexibility, necessary to be able to do the short circuiting. If it takes fewer than 9 comparisons to finish an output, further ones end up just comparing to salt, which never forms quintessence.
If this were the winning idea, it would end up getting a lot more attention. However, Bambi got 19th, and nobody else used KMP. 55 slow comparisons won’t win, if you can do 72 fast ones.
Faster comparisons
If we were to cut the time required for a comparison down, naïve 72 comparisons still has a chance. Not only a chance, but it could even be the better choice. KMP will always have a little bit of downtime between comparisons as you determine what is the next pair to compare. Naïve algorithm gets around that, as the comparisons can be queued up and run back to back (or, as we will see soon, even at the same time!). So let’s start to look for faster comparisons.
In my demo, I used 30 cycles to do a comparison, and the competitors with 1728-ish cycle solutions used 24. The fundamental limit of pairs as described is 18. To see this, note the unification glyph requires all atoms on it be dropped, after which they must be grabbed and moved again, leading to a 3 cycle cadence. Doing 6 separate checks would then take 18 cycles.
What’s challenging about getting down to 18, is the fact that your atoms get consumed when making quintessence. If you are relying on those atoms to provide a valid future test, you need to replace them, and the salt input can only provide an atom every 2 cycles.
JonJon found one way under 24 using an extra hex arm below the input to guarantee salts when needed. This led to a 22 cycle comparison and netted him a few placements.
Of the rest of the competitors, I think anyone who got under 24 got under 18 as well, largely thanks to parallelism.
Parallelism
Use more unification glyphs!
The most impressive parallel-pairs solution was by wchpsh, coming in 7th overall with 1108 worst-case weighted sum.
At a blazing 450 cycles, this takes 5.5 cycles per comparison on average, way under 18! It does this by running two separate computations in parallel across 3 unification glyphs each, so per-glyph it is 33 cycles per result. But in a really slick way.
There’s a neat trick in this that lowers the dependence on the salt input. The atoms flow left to right, and any quintessence formed is placed in the hole it leaves. As a result, when one unification glyph creates quintessence, the ones to the right of it no longer have valid inputs. wchpsh coordinates it so that these are the exact comparisons that don’t matter if there was already a no match. If the substring doesn’t match on an early character, then you don’t need to know if later characters match, so sabotaging their result is irrelevant.
Similar pairs-but-parallel approaches were done by tw33dl3dee, geco, fiesta0618, GoodbyeGalaxy, Kazyan, and Bist. Each had their own interesting implementation details, I urge you to watch the video to see them.
Separate fire check
There’s another way to speed up comparisons. Fire filtering is a method that I considered heavily when designing my own solutions. If we have access to a known fire and a triplex glyph, we can separate out the three options:
- Both atoms are fire (definite match)
- Neither atom is fire (possible match)
- One atom is fire and the other is not (definite no-match)
The three cases where neither atom is fire are handled by unification, taking a total of 9 cycles and making up the bottleneck. Everything else can be done separately.
I built this solution using fire filtering, which would have scored 6th right ahead of wchpsh if I hadn’t improved by switching tactics later. It gets somewhat close to the 9 × 72 = 648 cycle theory limit for this approach.
I also considered a parallelized version of this with more unification glyphs, but realized partway through that the cost would be high enough to make it worse overall. In the end, the only fire-filtering solution to appear in the final results was Haxton’s non-scoring entry.
Things that do not resemble pairs
Now it’s time to review two totally different approaches to the puzzle. Both of these approaches are substantially worse when applied to the single atom comparator puzzle. But they secured top spots among the solutions to Habitability Detector. They require some large number of comparisons for their power to shine.
Recall how in pairs we couldn’t tell the difference between e.g. air + air or earth + earth, and it didn’t matter. In what remains, it now matters what type the atoms are. But the benefits are absolutely massive. Let’s start with lock and key.
Lock and Key
If you’re familiar with a tumbler lock, you may recognize this image:

The key will only turn the housing, if it has the right indents to match all of the pins. If any single pin is not pushed to the correct spot (in the diagram, the key needs to make the red/blue interface sit right on the crease of the housing), then the key will not turn.
Now consider a key that has been specifically built to encode the long string, and a lock that encodes the short string. You can try that key at 4 different depths. One depth will test for a match to the first 3 atoms. One depth will test the next 3. And so on. (Note, real locks don’t have this ability because they stop the key at a very specific depth).
You are still performing the same 12 comparisons per output. But the method of comparison is inherently parallel. If done right, there is no need to back up to test an atom against a different part of the match pattern. To do the next trio of comparisons, just move the key one slot deeper and the existing information lines up differently.
In Lock and Key solutions, instead of using unification to perform the comparison, you use unification to convert individual atoms into some other form of information, some form that plays nicely with the parallelism embedded in Opus Magnum. Unification is now used for atom-checking, instead of pair-checking.
Theoretical efficiency
So how does one do atom-checking? And is it fast?
The goal is for there to be 4 different outcomes, corresponding to the 4 possible atoms. In this example, unification tests for earth first by placing water + fire + air on the other 3 slots. Then it tests for water by shuffling things around, removing the water and adding an earth. Then it tests fire, then finally air. Every success forms a quintessence (note: this is the opposite of pairs, where quintessence meant no-match!). The timing of that quintessence can be used to modify control flow within the solution.

Much like with pairs, you can add extra unification glyphs to get this to be a faster operation, or use triplex bonding to distinguish fire separately. Additionally, since there are only 4 possibilities, if it isn’t any of e.g. earth water or fire, it must be air. So the cleanest implementation of atom checking would only do 2 unification attempts and one triplex attempt per atom.
In the context of Habitability Detector, building a lock requires 3 atom-checks, and building the 6 keys that comprise the samples requires 36 total atom checks. Instead of needing 72 comparisons, this method needs 39 atom-checks.
Example solutions
GuiltyBystander
While it doesn’t win any awards for compactness, this is the most clear example of lock and key that was submitted. The following is the 24th place solution by GuiltyBystander. FYI, as it’s hard to see what the inputs are in this gif, the videos show first a no match and then a matching example, both in steady state.
Here’s a video of the earlier part of the solution where it builds the upper structure.
The structure consists of three 6-atom-wide blocks, each with a particular arrangement of teeth below. There are two gaps, one in a known place and one which depends on the particular atom tested. These structures are the 3 pins of the lock. A passing “key” will be one whose teeth line up with the holes between the teeth at some offset.
Atom checks on the sample convert into the position of the quintessence atoms on the key. The ordinary atoms on the key are there to make sure that the machine doesn’t break when there is more than one matching offset.
The lower arm on the short track, only grabs if there was a perfect match. The resulting shift causes the output on the far left, to happen for a gold atom instead of the salt atom.
Coocoo52
Coocoo52’s 13th place solution was titled “My brain hurts”. It takes lock and key, but wraps the key circularly instead which allows a lot more reuse of parts.
On the right is a big hexagon with a gold spine. Three of its edges have spokes. The position of the spoke along the edge depends on type of the match pattern atom. This one is the lock.
In the center is another big hexagon using extra match patterns as a spine. Atoms added onto it as spokes also depend on the atom type. This one is the key – if an atom matches up with the lock, the gold hexagon moves differently and an atom gets sent upward for processing.
Note that unlike GuiltyBystander’s implementation, this does not do all the comparisons in parallel. The lock and key have to spin to test one pin at a time, and combining this information happens in the top right by counting the number of successes.
I’ll also call out that the unification and dispersion combo on the left is a very efficient way to do atom checks.
rebix
This solution is conceptually the most similar to the winner of 2021’s binary subtraction puzzle. It encodes the problem in binary, with fire as 1 and salt as 0. This means it first builds a lengthy salt stick, then duplicates fire into 3 specific positions of the stick which depend on the match pattern. In the two videos below, the first long stick encodes “earth air air”, and the second one encodes “water water fire”.
Arms move fire atoms into locations below the stick. Atom checks move the stick an amount depending on the atom. Then it tests whether fire lines up with fire. A match advances one station to the left, a no-match goes to the waste chain.
Three comparisons happen in parallel, but it’s a different parallelism to GuiltyBystander’s. In GuiltyBystander’s solution, the offsets each were evaluated as a group, with 4 total groups:

In rebix’s solution there were 6 groups, all sharing the same S:

Regardless of the offset, a test fire would have to survive 3 consecutive groups to be counted as a success.
With 1367 weighted sum, rebix’s solution (titled “McDonald’s Ketchup Packet”) took 9th.
kaliuresis
In the previous post I gushed about kaliuresis, the strongest performing new competitor with a chance to win. His chance relied on a strong finish in the week 8 puzzle. Namely, he had to beat PentaPig by multiple placements. He rose to the challenge, delivering the 2nd place solution and one of only two solutions to have a weighted sum under 800.
This solution by kaliuresis, titled “Speeen”, shows that lock and key can be very fast. At 6 cycles per atom check, and doing only the 39 necessary atom checks, this comes in at under 300 cycles. This was the fastest submission of all.
The atom checks use two unification glyphs and a triplex, and they distinguish the 4 atoms in a very clever way. A hex arm constantly pivots an atom on a bonder. The 4 atoms all arrive at the other side of the bonder with a different number of cycles delay, leading to different orientations as they proceed along the rest of the solution.
The first 3 results, corresponding to the match pattern, go to the upper layer of the solution to become the lock. Here they spin in place. All subsequent orientation-encoded checked atoms spin by at the various stations of the hex arm. In the up-left position, it compares vs the lock. The grouping is the same as rebix’s – the three match pattern atoms all compare to the same sample atom at the same time. If they match, it propagates fire to the spinning lock, which then moves a test fire from one triplex bonder to another.
So while Coocoo52 wrapped GuiltyBystander’s offset-based grouping into a circle, kaliuresis similarly wrapped rebix’s staggered grouping, leading to an incredibly fast and elegant solution.
Lock and key wowed the crowd, but it wasn’t the winning method.
Complements

We’ve now seen how you can build structures differently in response to atom checks. What if that structure was “the other 3 elements that aren’t this one”? A single atom check, where earth would create the trio of atoms “water, fire, air” in response. Water would create “fire, air, earth”, and so on.
If you do this, then by the time you get to the sample you no longer need to do any atom-checks. You can place your dynamically-generated trio on the unification glyph, add the sample atom, and a match will create quintessence. This brings you back to 72 comparisons, but they take one unification each.
This sounds powerful, if you do it effectively. But, early in the week, I discarded this idea as too slow. What was I missing?
Well, the process of building these trios in response to atom checks, is not very quick or elegant. It’s cumbersome. I thought that you would use up the trio on the unification glyph. Once it’s consumed, you would have to start the whole process again..
Duplication glyph
I was completely wrong.
You don’t have to place the original trio on the unification glyph. Duplication allows you to copy any element onto salt. You can keep the original trio around to produce more copies, and use those copies for the unification check. This is what I took a while to realize, and what makes complements the strongest approach of all.
Because the match pattern never changes, complements of the match pattern, used for copying, are incredibly powerful.
Alternative approach by Starficz
I have to mention, Starficz managed to build a complements solution that did not duplicate the trios, and also did not regenerate them. He somehow found a way to preserve them by very particular ghost atom routing. I do not envy the struggle he faced to do this. In my notes about each solution I just write “complements but horrifying” for Starficz. His solution is shown below, but I don’t think I can spend the space in this post trying to make it make sense.
Instead, let’s take a look at the 5 players in the top 6 who used complements, and did use duplication.
Morraconda
Coming in 6th place with 990 weighted sum, is this solution by Morraconda:
She does gripe in the title about how this approach is “Forced 6P hell”. 6P means that the instructions placed by the player span the entire operation of the solution, rather than allowing things to loop. In a previous post we called this 6T instead; the term has changed by community agreement and P now means Products [per execution of the instruction tape].
Due to the 6P requirement, we have to view the different stages of the solution behavior separately. Above was the steady state, in which the length-two hex-arm is responsible for duplicating the trios, and the left half of the solution is busy running unifications. Below is the setup, during which the left half of the solution is completely idle and the goal is to make those trios in the first place.
These things are rather instruction-heavy due to the 6P requirement, but the method itself saves a lot of cycles without needing an excessive amount of machinery. Coming solutions only get more efficient than this.
Transcendental Guy
This one’s real fast. 36 cycles per sample, the same steady state speed as kaliuresis managed. Generating complements takes a little longer than setting up lock and key, but since transcendental guy has 3 different unification stations it is quicker than most. The overall cycle count is 330:
And the set-up where the complements get made in the first place:
In contrast to Morraconda’s hex-arm that holds the complements all in one location, this solution spreads them out across 9 separate duplicators. Each station holds a unification glyph, a dispersion glyph to recover new atoms from the quintessence, three calcifiers to turn dispersed atoms into salt, and three duplicators to regenerate that station’s complement.
Hex arms deliver atoms to each of the 3 stations – if unification succeeds, the atom is consumed. If the hex arm reaches the end of the track with no atoms in it, then a gold atom’s position reflects that information and the machine knows there was a match.
Every matched atom also causes there to be one new piece of waste. This is because dispersing quintessence yields 4 atoms, while there only need to be 3 to regenerate the complement. Morraconda’s solution generated waste too. Disposal is available, but it is not always economical to try to dispose all of it. This becomes something to try to optimize..
Kevelairn
Kevelairn’s 4th place solution showed us how it’s done. A fast, wasteless complements solution at 36 cycles per sample, using a single unification glyph.
And here’s setup. Note that the trios held by each arm are not one complement each. Instead, immediately after it is computed, a match pattern atom’s complement gets distributed one atom to each arm. 3 match pattern atoms, 3 atoms per arm.
The steady state speed of 3 cycles per unification is impressive. It really streamlines the process of recovering the complement. If unification is successful, then the dispersion glyph creates 4 elements as before and the extra one is right next to disposal. If unification is unsuccessful, then the 3 atoms from before are cleanly reused. The logic for counting to 3 matches and selecting the output, takes place right next to disposal as well.
There’s one more trick to achieve wastelessness here, and it takes place on top of the single atom salt input at the top. Kevelairn’s solution duplicates from the sample using hex arms at the top, meaning the original sample atoms become waste in the end. To discard them, Kevelairn pushes them onto the input on the same cycle the hex arm takes an input. This allows the input to serve as a disposal glyph too. A useful trick with these high activity solutions to keep them wasteless. We will see more of this later!
PentaPig
In 3rd place with 817 weighted sum was the tournament winner PentaPig. By being within a placement of kaliuresis, he stayed in the lead overall to take the tournament. That on its own is commendable, but let’s see how he approached the puzzle:
A “slower” 48 cycles per input, taking 4 cycles per each unification. But it is much faster to set up than the previous solution, so it recovers almost all of the cycles, while gaining tremendously on cost and area. The setup does the same thing as Kevelairn’s, distributing each complement across 3 arms, one atom apiece.
It is also wasteless, using the disposal for atoms of the sample as well as atoms from the count-to-three mechanism at the top. Test atoms which attempt to match but fail, return directly onto the salt input. Complements recover via dispersion. This is overall remarkably similar in concept to Kevelairn’s solution, while having a significant difference in look (and better score) due to the layout.
The winner
Time to toot my own horn. I’m still pretty good at this game, as it turns out.
To beat all of the previously shown solutions, I built the following, titled “pinwheel”.

And on a version of the puzzle with matches (where it outputs 4 cycles later and gets its worst case stats):

This is a complements solution. The titular pinwheel has three three-atom spokes, and each one is one of the complements. When it chops downward onto the held salts, they become the copy and carry the information upward to test against the sample.
Like PentaPig and Kevelairn, I also use an input as a conditional disposal. Unlike them though, I use the match pattern input in this way. With a reminder – in these complements-style solutions, the existence of the complements makes the match pattern obsolete, basically a fancy salt input! Nothing ever needs that information in that form again.
This prevents the need to disperse quintessence – I can dispose it directly. I get the 3 atoms I need from the match pattern. If I still have the 3 I started with, then one suppresses the match pattern, which doesn’t show up.
I also don’t need to dispose of the atoms from the sample. The layout of the trapezoid track at the top means it can interchangeably make a copy or take the original from the sample as needed.
I’ll say more about the solution and its predecessor soon, but I first want to make a remark about scoring.
Weighted sum
This solution has 748 weighted sum. The weighting “cost/5 + cycles + area” really makes cost less important than cycles or area, but it isn’t unimportant. When comparing this solution to PentaPig or kaliuresis, where I win is by being significantly cheaper. Each beats me on cycles + area, but when adding in cost/5, they lose their lead and more.
I naturally play this game in a very cost-conscious way, but I don’t seek out cost as a primary metric. These sorts of weighted sum metrics where cycles is still supremely important but you can’t break the bank, have appealed to me. I think it’s interesting how in both 2021 and 2023 my wins in the computation puzzle (with this metric) have been with the cheapest of all the “fast” solutions.
A few decisions cheapened this vs the ones shown before. The pinwheel itself is one structure, taking fewer mechanisms to use and control. It sits fully in the control of one of the arms that made it, leading to no added expense there. I think my salt/gold selection logic is pretty slick as well. It’s not much, but instead of testing for successful matches I test for unsuccessful ones, and it happens in-passing by the arm that is already bringing that extra atom to disposal. As a result, it doesn’t take many extra arms or bonders to complete the puzzle from there.
There are a few components with no use at all in steady state. So let’s see how I used them in setup.
Setup
There’s enough intercommunication possible between useful parts of the solution, that I didn’t need to add much. But there needed to be a dispersion glyph (the only way I could find to build complements at all), and arms to service it. There needed to be a berlo on top of one of the useful duplicators, so that I could place known elements. And there needed to be a quick way to get from one side of the unification glyph to the other, so I added a length 2 arm that sort of dinks around in the middle in steady state looking unused. All of these components pay for themselves with speed during the setup phase. With them, I’m able to score a lower cycle count than Kevelairn while having a 48 cycle per input steady state to his 36.
There are 2 atoms of garbage that sit awkwardly on the board after setup. There is a 3rd atom which would have that fate, but it’s actually the center of the pinwheel!
Why does the pinwheel spin the wrong way sometimes
You might have noticed this, and I suspect it would bug people enough that I want to pre-empt questions about it by providing the answer.
It’s a weird consequence of the programming of the hex arm that holds the sample atoms. It needs to load the next input at a particular timing, and as a result the first 3 comparisons happen in a different order. In simple terms, a pinwheel that only spins one direction will supply 123 123 123 123 forever. This one needs to supply 231 123 123 123 231 123 123 123 etc. So it spins backwards once to get from 3 to 2, and holds still at one other point to stay on 1.
The parent of Pinwheel: Big Triangle
My first complements solution, after abandoning fire-filter and an unfinished parallel-fire-filter, was the following:
Many of the parts carried on into the winning solution, but it does a few things notably worse. The counting-to-three logic requires so many more arms, and disposing sticks of unknown length is clunky.
If we look at setup, the berlo is really awkward. I need 3 duplicators just for berlo and it uses quite some time to create the test patterns for setup.
And, purely aesthetically, while the big triangle is pretty, it isn’t quite as flashy or centralized in the solution, as the pinwheel is in the successor.
Remarks
If I had stopped at big triangle, and its mid-800s weighted sum, then kaliuresis would have won this puzzle with lock-and-key. So while complements took 1st place and made up 5 of the top 6, it could very well have been implementation details that made the difference. Opus Magnum is no ordinary computing landscape. It takes cleverness, geometry, and some persistence to make a great idea into a great solution.
The 2024 tournament is coming very soon, check the events website for puzzles after January 1st! Zorflax is the host this year. He will be using the same scoring system as panic did in 2023. However, Zorflax is a famed hater of computation puzzles. Instead of ending this next tournament on a computation puzzle, he will be doing “something different”. Even though I love computation puzzles, I still look forward to what that might mean..
Thanks for your patience as I promised this blog post way longer ago. I know a few of you have poked me in the time since, asking when it might see the light of day. Truth be told, in early April I had around a third of this already written, got into the complex Habitability Detector solutions, and just felt burned out. And 2023 has been a hell of a year for my life in general. I tried to get back into writing in June and couldn’t. I think, with 3 posts in December, I’ve made it back. There may be another before the year’s end, so stay tuned.
I appreciate you all! Take care and see you next time.