Revisiting Number Theory and the Impossible Puzzle
A couple years ago I wrote about the impossible puzzle, also known as the “sum-and-product puzzle” or “Freudenthal’s Problem”. That post was also my entry for the Summer of Math Exposition, where I placed in the top 100. I do recreational mathematics as a hobby, and this problem is one of my long-standing fixations. I’ve put many hours and CPU cycles into this problem, and have a number of original results to share. This post contains many of those results. But first, a brief refresher!
Alice declares “I am thinking of two whole numbers greater than or equal to 3. I have told their sum to Sam, and their product to Polly.”
Sam says to Polly “You don’t know the numbers.”
Polly replies “That was true, but now I do.”
Sam responds “Now I do too.”
Classify all possible pairs of numbers.
What We Learned Already
For this puzzle, the key piece of information to make progress is contained in the line “you don’t know the numbers”. In being able to say this, Sam reveals that their number (the sum) belongs to a specific infinite set we called S.
We then defined a function F. For any number s in S, the next line said by Polly is possible F(s) different ways. We called the graph of this function “Freudenthal’s Comet”, in relation to Goldbach’s Comet in a more famous number theory context. Freudenthal’s Comet looks like this:

When looking for solutions to the puzzle, we are interested in s where F(s) = 1 exactly. Only when F(s) = 1 can Sam say the final line. Most often though, F(s) > 1. It’s actually quite rare that F produces low values.
When talking about solutions, I will equivalently talk about values of s. This means that the canonical solution (13, 16), will be called 29. No two pairs of solutions can have the same sum, which should be clear from the final statement by Sam, so this loses no information. This also lets us talk about the smallest solutions without ambiguity as to the meaning of the word “smallest”.
Magical Moduli
In the last post, we looked at the smallest several thousand solutions. We can glean some information about their tendencies modulo small primes. In addition to being odd, every single solution is 2 mod 3. Oddness is not surprising, as if Goldbach’s Conjecture is true, even numbers are always the sum of two primes and so cannot be in S. The latter is more interesting. We separated out Freudenthal’s Comet based on the class of s mod 3:

The lowest branch, which contains the only cases where F(s) = 1, happens when s is 2 mod 3.
In the conclusion of the previous post, we showed that the comet is not just 3 branches. It has a fractal-like nature, where the branches themselves have branches. Sadly, we cannot use computers alone to generate enough data to see them. We needed to put on our mathematician hat and start discussing solutions that were much much larger. To do this, we looked at how certain s with specific modular properties, are “protected” against large F(s). That is one concept I want to dig much deeper into with this post.
Patterns and When They Fail
We will look at patterns that hold for a long time but then break down, which is one of my favorite phenomena in recreational mathematics. Recall the chart from the previous post, where the most common even number in a solution pair was 16:

We will talk about the reason that 16 is so prevalent, and also why there may nevertheless be a largest solution to have 16.
For another broken pattern, look at the histogram of solutions mod 5 as we include more and more small solutions:
Unlike the classes mod 3 where every solution was the same, things are a little more diverse mod 5. It’s not a flat distribution though; there are many more solutions 4 mod 5. Our canonical solution with s = 29, is a representative of 4 mod 5, which seems to have a comfy lead over the other classes. However, in the infinite limit, it is the 1 mod 5 class that has infinitely many solutions, while the other classes each appear to have a final, largest solution. We will try to determine around what magnitude those solutions are.
To get started, we first need to understand something about the prime numbers.
Probability and Primes
Let’s consider an experiment. Imagine a random number generator that produces 3 digit numbers, every 3 digit number equally likely. We ask this machine 5000 times to give us a number, and then count how many times we get a prime number.

The graph above reflects doing this experiment itself 1000 times (hence 5 million different uses of the generator), and collecting the total number of primes in each independent run of 5000. A statistician will see this and think of a probability distribution. There are 900 different 3 digit numbers, and 143 of them are prime, so the expected value is 5000 * 143/900 = 794.4. The standard deviation can also be computed using the binomial distribution, and comes out to around 25.85.
How about if you repeated this experiment but your random number generator could only produce 4 digit numbers? 5 digit numbers?

(by the way, shoutout to my Wolfram Cloud notebook for prime checking 5 million 9 digit numbers so quickly).
What we are building here is a sort of visualization of the prime number theorem. The prime number theorem makes a statement about the density of primes in the integers. Primes are less common as the numbers get bigger. Taken as a statement of probability: the probability that a value N is prime, is 1/log(N).
A Reasonable Objection
You may find it odd to give a probability that a number is prime; after all a number is prime or it isn’t. Given any integer, such as 123456789, we can know with certainty whether or not it is prime by factoring it. 123456789 is composite because it is divisible by 3. The statement that it has a 5.3% chance of being prime, is ludicrous.
However, if your view of the integer is not sharp enough, and instead of knowing it as an exact value you know only the vague “size”, it quickly becomes a question of probability. This applies when looking at the set of “9 digit numbers” for example. Without actually knowing the number of 9 digit primes, we can estimate that since the average 9 digit number is about 108.5 and the average 3 digit number is about 102.5, the ratio of their logarithms (in any base, although the theorem uses base e) is 2.5/8.5. Thus the peak of the distribution for 9 digit numbers falls at around 2.5/8.5 * 794.4 = 233.7. The graph agrees.
I hope that this demonstrates the predictive power of the probabilistic treatment of primes. Because now we are going to throw modular arithmetic into the mix.
Known Factors
Returning to our experiment, now assume that the generator can only produce even 3 digit numbers. In this case, there will never be a prime in its output. The presence of a known factor completely eliminates the probability. But what about if it can only produce odd 3 digit numbers?
Well, the earlier distribution contained both even and odd numbers. With so many samples, we expect that very nearly half of them were even, and the others odd. If the even numbers are never prime, then the odd numbers have to make up the gap, making them twice as likely to be prime. So the distribution would be centered around 2 * 794.4 = 1588.8. Which it is:

In the more general case, suppose that we know our number N is not a multiple of some prime p. Since 1 in every p values is a multiple of p, this information makes our N a factor of p / (p – 1) more likely to be prime. A slightly stronger form of the prime number theorem states that primes are equally likely in all of the congruence classes, so knowing that N is, say, 1 mod 3 rather than 2 mod 3, makes no difference to its probability.
So, if we do our number generation again, but restrict our random numbers to be always 5 mod 6, then we guarantee that they are not a multiple of 2 or 3. This boosts probability by an overall factor of (2 / 1) * (3 / 2) = 3, and so we expect counts (X axis values) three times higher.

In general then, when discussing the probability a number is prime, we have to consider its magnitude and any known factors.
Putting This to Use
Consider some very large s from the set S. How about we are handling a 1000-digit number, somewhere between 10999 and 101000. What is F(s), as a rough estimation? What sorts of promises would we need to make about factors of s or numbers near s, in order for F(s) to have a chance to be 1?
Possible Primes
Even if computing F(s) is out of reach, we know from the previous post that it goes up by 1 every time that four numbers are all odd primes:
- a
- s – 2ka
- 2k(s – 2ka) + a – 4
- a(s – 2ka) + 2k – 4
Here a and k are any positive integers such that s – 2ka is positive. There are around s possible assignments of a and k.
Depending on how carefully we choose to investigate this expression, we can come to a more or less useful answer. However, at the simplest level, these are 4 numbers that are around as big as s itself, so 1000 digits each. The probability a number of this magnitude is prime goes like 1 / log(101000) or 0.0004. The probability that 4 such numbers are all prime is the 4th power of this, or around 4×10-14.
It seems pretty unlikely, until you realize there are around s different ways to assign a and k, so s different chances to roll this 4×10-14 rarity. Suddenly we are looking at some 10986 expected successes, with a standard deviation of about 10493. And that’s just a lower bound on F(s). This is far far away from 1.
Even if we tried to get fancy and say that the first two numbers are always less than s and the next two might be a good deal bigger than s, we are not moving our result by 986 orders of magnitude. There is only one way we can meaningfully change our expected value of F(s) by that much. We need known factors.
Protection Against Certain Values of k
I am going to be using the word “protection” in this blog post as that’s how I conceptualize it. Here is what I mean when I say it. If some input s has protection against a value of k, then for that k and all a, there is precisely 0 chance all 4 expressions are prime. This will be due to known factors in one of the four expressions.
For example, expression 4 reads a(s – 2ka) + 2k – 4. If k = 2, then it simplifies to a(s – 4a) which is obviously divisible by both a and s – 4a. Those are the first two expressions, so if both of them are prime (and thus not 1), then the final expression must be composite. k = 2 is a universal protection, not requiring anything to be true of s itself.
How does that protection impact our estimate for F(s)? Breaking down our s different chances to roll a 4×10-14 rarity, half of them have k = 1, a quarter have k = 2, an eighth have k = 3, and so on. We got rid of a quarter of our chances, which doesn’t change the order of magnitude. But it’s a start.
When trying to cut F(s) down by orders of magnitude at a time, the most useful k to try to find a protection against is the smallest one remaining. The time has come for Fermat and Mersenne factors.
Fermat and Mersenne Factors
This puzzle has led me into many corners of mathematics and number theory. These numbers are a highlight of the journey. There are many reasons to care about factors of numbers that can be written as 2k + 1 or 2k – 1. Numbers of the former type are called Fermat numbers. They relate to constructible polygons, and it’s widely believed that none are prime after 65537. Numbers of the latter type are called Mersenne numbers. They are infamous in prime hunting, and currently represent the 6 largest primes known to humanity.
In this sum and product puzzle, both of them play a star role. By manipulating the third expression from the previous section, we can write it in two separate ways:
- 2k(s – 2ka) + a – 4 = (2k + 1)(s – (2k – 1)a) – (s + 4) = (2k + 1)n – (s + 4)
- 2k(s – 2ka) + a – 4 = (2k – 1)(s – (2k + 1)a) + (s – 4) = (2k – 1)n + (s – 4)
Here n is a useless integer, there only to show that that particular term is a multiple of a Fermat number (first case) or Mersenne number (second case). It follows that the third expression will always be divisible by both GCD(2k + 1, s + 4) and GCD(2k – 1, s – 4), where GCD is the greatest common divisor function. These divisors are guaranteed, regardless of our choice of a.
If both GCD are 1, then this fact is useless. But if we choose s to have specific modular properties, we can make many of these GCD into fully fledged factors, which means they can provide protection against k.
k = 1
The most impactful k to eliminate is k = 1, as it accounts for over half of all our chances to roll 4 primes. The small k correspond to the smallest Fermat and Mersenne numbers. However, the Mersenne number corresponding to k = 1 is itself 1, and so the GCD can never be a useful factor. This means that to protect against k = 1, we must use the Fermat condition: GCD(3, s + 4) > 1.
Simplifying, s must be 2 mod 3. This condition is familiar; when we protect against k = 1 this way, we end up in the lowest of the 3 branches of Freudenthal’s Comet. We have reproduced the argument we already know applies to all existing solutions.
k = 3?
Since we get k = 2 for free, the next k we have to care about is k = 3. Notice that the 3rd Fermat number is 23 + 1 = 9, which is simply 3×3. We already have GCD(9, s + 4) = 3, a nontrivial factor. Put another way, Fermat protection against k = 1 has guaranteed us Fermat protection against any k where 2k + 1 is a multiple of 3. So which k are those?
Consider the exponent (2m+1)k, that is to say, any odd multiple of k. The corresponding Fermat number is 2(2m+1)k + 1, and we can factor this. It factors as (2k + 1) × (22mk – 2(2m – 1)k + 2(2m – 2)k – … + 22k – 2k + 1). The signs in the latter factor alternate, and the first and last must both be positive. Accordingly, this rule only works for odd multiples of k. Even multiples of k have no guaranteed factors, and may indeed be prime (22 + 1 = 5 being an example!)
This identity means that whenever we protect against any k using a Fermat condition, we get all odd multiples for free. The odd multiples of 1 are all the odd numbers, so they are now already covered.
The Mersenne condition has a similar factorization identity, but it applies to all multiples. Looking at 2mk – 1, we see that it factors as (2k – 1) × (2(m – 1)k + 2(m – 2)k + … + 22k + 2k + 1). The signs do not have to alternate. This rule means that a Mersenne condition protecting against k, also protects against every multiple of k. But remember, we only get a nontrivial divisor when k > 1.
The Covering Game
If our goal is to reduce the initial estimate by 986 orders of magnitude, we need to cover all k up to around 3275. That leaves about 1014 remaining assignments for a and k, enough to expect just about 1 hit on the 4 prime roll. What kinds of factors does it take to cover that many different k?
We showed in the previous blog post how for s larger than around 265, there is a sequence protected against all k. I’ll call this the big hammer strategy. We could definitely use the big hammer. For any s that is 6705290747541849491 mod 36893488147419103230, a combination of Fermat and Mersenne factors properly eliminates every single k. But that gives us no chances to roll 4 primes. For various reasons we will get back to later, this is not a terrible thing. But it is not what we are looking for.
Precision Covering
How precisely can we “stop” our protection on a target value? Since k = 1 has to be protected, and the only way to do this eliminates all odd k, we can only ever hope to stop on even k. Going up one from 3275 gives 3276, which is 2×2×3×3×7×13. Unfortunately, that is an odd multiple of 4. Whether we protect against k = 4 using Fermat or Mersenne, we will catch k = 3276 in the crossfire either way. It is not possible to cover everything up to 3276, then let 3276 remain unprotected.
Going one down from 3275 gives 3274, which is 2×1637. This is an odd multiple of 2. Remember: we don’t need to protect against k = 2, that protection came for free! It would be possible to cover everything up to 3274, and then let 3274 remain unprotected.
To do this, we must individually cover every k which is twice a prime. Unlike the big hammer strategy that covers every single k with a small number of factors, a precision covering needs to come up with separate factors for 4, 6, 10, 14, and so on.
I find this delightful: the fact that k = 2 comes for free gives multiple options for how to go about keeping F(s) low. It makes precision coverings possible at all. The benefit of a precision covering is that it allows fine-tuned control over the number of chances to roll 4 primes. Whenever a precision covering exists, solutions will be far more probable.
Does Fermat vs Mersenne Matter Here?
Say we protect against k = 4 with a Mersenne factor. In doing this, we cover every multiple of 4, so the only k that remain are odd multiples of 2. Then when we move on to k = 6, it won’t matter at all whether we use Fermat or Mersenne. If we use Fermat, we don’t cover even multiples of 6, but all even multiples of 6 are multiples of 4 as well. The same is true for all of the remaining k.
However, if we protect against k = 4 with a Fermat factor, then we leave multiples of 8 uncovered. This would mean that those each need special care. A slightly weaker form of the big hammer strategy can eventually get back to complete coverage of multiples of 4, but it’s a far better usage of factors to simply use Mersenne to cover k = 4 in the first place. In what follows, I’ll assume that k = 4 is covered via the Mersenne condition GCD(5, s – 4) > 1.
Chinese Remainder Theorem
As long as we never use the same prime factor twice, we can assemble all of our conditions into an arithmetic sequence. This is guaranteed by the Chinese Remainder Theorem.
The only factors we have used so far are 2 (s is always odd), 3 (protecting against k = 1 using Fermat) and now 5 (protecting against k = 4 using Mersenne). Assembling these, we find that s must be 29 mod 30. This means that of the roughly 101000 1000-digit numbers we could have started with, only one in 30 meets this condition. That’s hardly an impactful restriction, for now.
Now let’s add more factors for all the k = 2p. At each point we want to pick the smallest factor. Doing this preserves the most s. However, we cannot ever pick 3 for Mersenne, or 5 for Fermat. This would be incompatible with our previous conditions, and violate the Chinese Remainder Theorem.
Numbers to Factor
Let’s start with k = 6. We want to find a small prime factor of either 63 (that is not 3) or 65 (that is not 5). The clear answer is 7, as it is the smallest available factor. It divides 63, so we would introduce a Mersenne condition GCD(7, s – 4) > 1. I’ve been writing these conditions as a GCD, but really since the number is prime it’s identical to saying that s is 4 mod 7.
For k = 10, we want to find a small prime factor of either 1023 (that is not 3) or 1025 (that is not 5). The clear answer is 11, as it is the smallest available factor. It divides 1023, so we would introduce a Mersenne condition. s is 4 mod 11.
Having two numbers to factor is a little cumbersome. The first one is always divisible by 3, but we cannot use the 3. The second one is always divisible by 5, but we cannot use the 5. And we need to factor both of them, just to compare their smallest factors. We could instead factor their product. Certain factorization methods do not care how big the number is, only how big the smallest factor is. In our case, we are looking for the smallest factor anyway, so it saves computing power to first multiply the numbers together and divide out by 15.
The product (22p – 1) × (22p + 1) is 24p – 1, another Mersenne number but now with an exponent of 4p. It is for this reason I became very interested in the factors of M4p/15 for all p.
Computer Aided Factoring and Prime95
The Great Internet Mersenne Prime Search, or GIMPS, was established in January 1996. It uses distributed computing to search for Mersenne numbers which are prime. Over the years, the underlying software known as Prime95, has added new features for related tasks. If I was interested in factors of M4p, the best place for me to start was by downloading Prime95.
For most “small” exponents, there’s hardly any work needed. Because I’m pretty familiar with using Wolfram cloud notebooks already, I wrote a one-liner to give me the 258 factors needed to cover up to k = 3274. I was pleased to see the whole computation take 13 seconds:

Once we get to even larger exponents, I can have Prime95 search for small factors in an intelligent way. But I can avoid even that – there’s a website factordb.com where I can see whether anyone has ever uploaded a factorization. These will come into play later. For our current goal of finding thousand-digit solutions, the exponents are still comfortably in the range of “small”.
How Restricted Are We?
Let’s assemble our modulus using the Chinese Remainder Theorem. First we have to check that all of the values above are coprime with each other, and they are. Next we have to fix the third value which is currently 15 but should be 29 (this can only happen for 228 – 1 and it’s because I took a shortcut to get factors). Then we also add in the 2, 3 and 5 from before. Finally we multiply them all together and we get…
A 1005 digit number.
1 in roughly 4.33×101004 integers has the property that protects it all the way out to, but not including, k = 3274. The smallest one is approximately 2.07×101004.
None of our 1000 digit numbers have the necessary property!
This is the flaw of precision covering. There is a race, and here at 1000 digit values we find ourselves on the losing side of it.
There is a single 1000 digit number which is protected all the way out to, but not including, k = 3254. This leaves around 1020 possible assignments for a, and we would expect around a million of them give 4 primes. This is too large for us to expect F(s) = 1.
Winning vs Losing
There’s a clear question here. How often are we winning vs losing this race? Let’s dig in.
We are winning whenever we can protect out to but not including a given k, without needing to be much bigger than 2k. When this is the case, we have the fine control that a precision covering can offer. We are losing whenever the numbers protected out to k are all far larger than 2k. When this is the case, no values of s have adequate protection, at least not with this strategy.
We can make a logarithmic plot of s, and color regions based on whether our best possible precision covering is winning or losing in that region:

The Y axis states the margin in orders of magnitude (base 10). We can see that winning is the norm for quite a while. Then somewhere around 10400, it becomes a rarity. These values need to protect against k = 1226, 1234, 1238, each using a separate factor. For 1226, that factor is unusually large, at 17458241. Not much further to the right we encounter k = 1282, 1286, 1294, another cluster with separate, often large factors. These clusters push us down into the red.
We start to gain back some ground whenever there are large prime gaps. Since the graph can only go down when k passes 2p, gaps help the cause. It’s also nice whenever the 2p we do pass only require small factors. For a brief moment around 850 digits, we are winning again. Then we get plunged back into the red by k = 2846, 2854, 2858, and 2866, each of which needs its own factor.
Relationship of This Graph to F(s)
Every point on the graph corresponds to the start of a new arithmetic progression of s values. At these starting points, we can estimate F(s). If the graph is above y = 0, in the green, then every k is protected and only edge cases like (16, p) can show up. If the graph is below y = 0, in the red, then there are a number of ways to express s as 2ka + b using an unprotected k. The number of ways is 10–y, so at the right side of the graph we are looking at 1020 possible assignments.
The assignments are only a contribution to F(s) at a very low probability. The actual estimated value of F(s) would take this graph, multiply by a factor of log(s)4, and then turn it upside down.

It’s still on a log-log scale, so y = 2 corresponds to F(s) = 100, and strongly negative values like y = -10 corresponds to F(s) = (most likely) 0.
The Fractal Nature
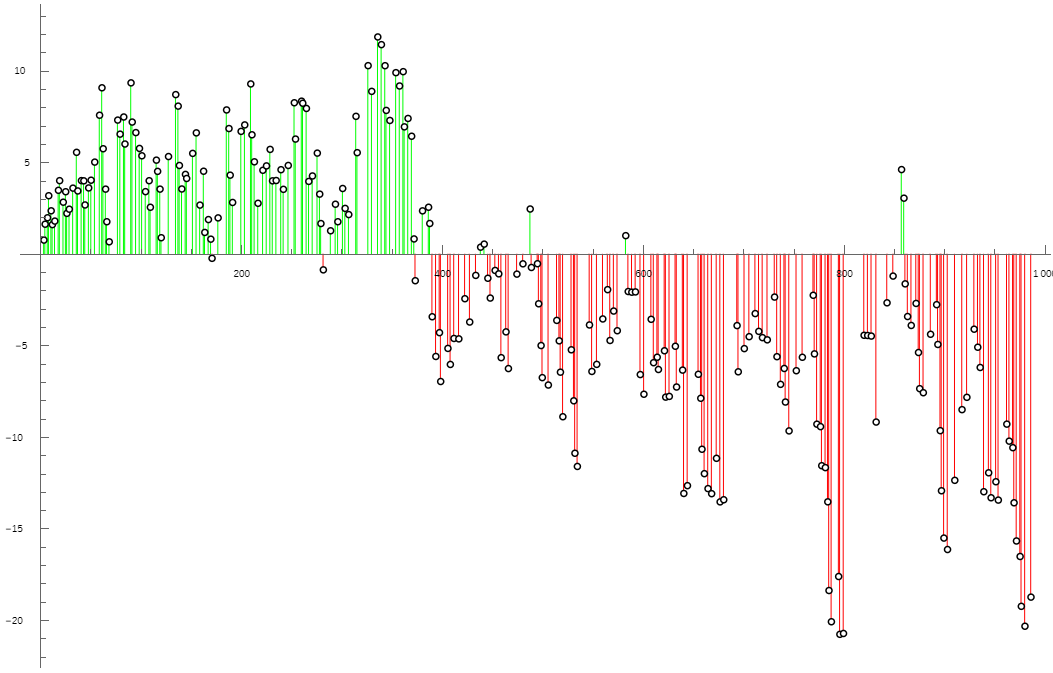
These chosen s values only start an arithmetic progression. Moving deeper into any of these arithmetic progressions, F(s) steadily climbs. This climb happens relatively steeply, so to get a good look we need to zoom way in:

All of the zero crossings correspond, with high likelihood, to many solutions. Once that progression has climbed too high, it never yields solutions again. Fortunately, it looks like we keep getting new ones below the line. Branches and branches galore.
Larger Still
Solutions are just barely out of reach at 1000 digit numbers. The precision covering strategy might still be able to claw its way back. Let’s extend our graph of the expected value of F(s) at each sequence start a little further:

Unfortunately, we start losing badly. F(s) starts each new branch already far out of reach. One big reason is that at k = 4534 we finally hit a truly terrible factor. To protect against this k alone, our best option is a Fermat condition using 434417855820434767471513. We lose two dozen orders of magnitude of breathing room, that we did not have to start with. That last little sliver of green before the cliff, corresponds to protecting against all k up to (but not including) k = 4534.
I’ve gone further with not-confirmed-minimal factors, and it doesn’t appear to recover. At least not before k = 20000. I don’t entirely trust my results though. The methods used to find factors of numbers this large, don’t promise that they always find the smallest factor. With Prime95 and factordb as my source, I could easily be missing smaller factors somewhere. However, I threw a lot of computer cycles at ECM on (29068 – 1)/15 and it does really seem like the big bad 434417855820434767471513 is its smallest factor.
Mod 5
Because of the Mersenne condition on k = 4, the sums on all of these solutions are 4 mod 5. That makes them the dominant bar in the histogram of known solutions. In fact, it distinguishes them from any big hammer solution, which shows up in 1 mod 5 instead.
It’s worth trying to understand where the handful of 0, 2, and 3 mod 5 solutions come from. If one uses the Fermat condition on k = 4 instead, there is no longer a reliance on 5 as a factor at all. But it incurs new factor requirements at k = 8, 16, 32, and 64. Thanks to these factors, it has a much worse chance to produce solutions:

Still, it is very occasionally green. At the start, and again at around 350 digit numbers. Protection against k = 1198 is what puts it over the edge for possibly the last time.
This is generally what it looks like if we try to use this strategy with suboptimal factors. We get more interesting congruences, but they are successful less often. They all hit the same wall at k = 4534 though. If any of them ever recover, it’s not for a long while.
The Actual Solutions
I’ve turned the whole thing into a game of coverings and strategy, a race between factors and exponents. It’s hardly recognizable from the original problem about dialogue and “you don’t know”. To me, the journey we have taken is beautiful. However, we must remind ourselves of Sam and Polly.
Returning to the numbers Alice conjured in the first place, we find that all pairs we have just worked to produce are of the form (4p1p2, p3).
p1, p2, p3 are odd primes; p2, p3 are additionally both 1 mod 3. Of solutions we found in the previous blog post, some had this form. For example, (19456, 483883) has p1 = 5, p2 = 19, p3 = 483883.
It seems solutions of this form are extremely prolific for a while, but then stop appearing. Somewhere, possibly with the form (24534p, q), is the largest solution that this strategy permits. The largest solution whose sum ends in a 9. The largest solution with an “exotic” power of two.
Maybe with enough computing power, we can find that solution. Just to say hi.
Beyond it, I believe that a different strategy is necessary. The powers of two that can appear in a solution become restricted, only permitting 64n or (64 × 2n) + 2 (as the exponent itself). The sums are always 232 – 5 mod 233 – 2. Let’s finally look more closely at the big hammer.
The Big Hammer
As we described in the previous post, protecting against k = 2 with a Fermat condition means that one cannot protect against k = 4 with a Mersenne condition, and so must use another Fermat condition. Similar applies for k = 8 and 16. Because the associated Fermat numbers are all prime, everything is forced. Taking just these forced conditions, s must be 232 – 5 mod 233 – 2. In digits, we know the sum ends in a 1.
However, k = 32 is special. While we still cannot use a Mersenne condition, we finally have choices for our Fermat condition. The Fermat number 232 + 1 is composite, after all previous 22n + 1 were prime. So we can achieve GCD(232 + 1, s + 4) > 1 by simply having s + 4 be a multiple of either 641 or 6700417. With the other factor unused, we can use Mersenne for k = 64 if we want to.
If we use Mersenne for k = 64, we have employed the big hammer. There are no remaining k uncovered. However, other options exist.
Leaving a Hole in the Hammer
If instead we use Fermat for k = 64, then we let k = 128 remain uncovered. We can keep going, using a Fermat condition every single time we reach a power of two, and in so doing let the next one stay uncovered. So long as we don’t use a Mersenne condition, we leave a hole in the hammer.
This amounts to a weaker version of the precision covering, specific to k that is a power of two. But unlike the previous graphs, this one is always in the green. We run into new necessary factors so infrequently, that even if every single 22n + 1 were prime, the Chinese Remainder Theorem would still tell us that 22n+1 – 5 has the protection we need, which is notably 5 less than 22n+1, the first k we didn’t cover. Carrying the associated arithmetic progression forward, we can always choose to let the “right” amount of expressions s = 22n+1a + b through to have a chance to find a solution.
We expect a significant number of solutions that have 22n (n ≥ 6) as the even part of the even number. For each n, we get a few orders of magnitude where F(s) is reasonably likely to be 1. However, in the 1000-digit range (for example) where we previously wanted k = 3275, this is useless. k = 4096 is too large, and k = 2048 would let 10383 assignments slip through, leaving an expected F(s) around 10369 with a standard deviation around 10184. Even with a large number of s to play with, we cannot expect solutions here.
Still, solutions should exist in the 1250 digit range with k = 4096, then again in the 2500 digit range with k = 8192, and so on.
Power-of-two Plus Prime
Eliminating various k proceeds under the assumption that 2ka × b can be factored equivalently as 2kb × a. a = 1 constitutes an edge case here, since the factors need to be 3 or greater. This means one number is a power-of-two. Whenever the other number is prime, then the product has only one odd factor sum, instantly enabling Polly to say her line. Many of our early solutions took this power-of-two plus prime form, including the canonical (13, 16).
If we take our sum s and subtract off a power of two, do we have a chance to be prime? Well, our Fermat and Mersenne factors may work against us:
s – 2k = (s + 4) – 4 × (2k – 2 + 1) = (s – 4) – 4 × (2k – 2 – 1)
If using the big hammer, s + 4 and s – 4 are going to have factors in common with the term on the right in every case. Thus this won’t yield any primes with k > 2. We also know 4 + p cannot be a sum in the set S so we don’t have to worry about k = 2.
If we are leaving certain k uncovered though, assuming that we expect F(s) to be otherwise 0, then we may find solutions. The power of two would be k + 2.
This actually explains why 16 shows up so often! Our precision coverings don’t need to have any explicit protection against k = 2, so there are no factors guaranteed for s – 24. Wherever our graph is green we may also find (16, p) pairs. Once it turns red though, even the iconic 16 falls into darkness, crowded out by unprotected k.
Rapid Fire Examples
Looking much larger, I have found some possible solutions:
- (22050, 536533801808894140828183058584769005191020422475055090568282127137)
- (24098, 37435819635819699115196001918156276198735684498465800468745148067461477)
- (28194, 84287727152277473736309074761515872896678171102779735939739330681183719180547)
- (216386, 14089824971011252455443051181154819186800803143181763234075339130317926095692338082528097)
I found a 1380 digit probable-prime that could be a solution alongside 24536, but only if we fail 1015 chances to hit 4 primes. I found an 856 digit probable-prime alongside 22848, which has much better chances thanks to how much further in the green we were in that range. In the same range, I found an 857 digit probable-prime which would instead accompany 16.
Note: in this section and further, due to factoring being a hard problem, I’m content with “probable primes” according to Wolfram Cloud which performs a Miller-Rabin and Lucas Pseudoprime test. The probability that a number is flagged as prime despite being composite, is terrifically low but not 0%.
Power-of-two Plus Composite
Some of our original solutions had a power of two and a composite. This suggests that known factors of s – 2k do not prevent there being a solution. So let’s assume we have protected against all k, then consider the two alternate factor sums. Writing s = 2k + pq, we need 2kp + q – 4 and p + 2kq – 4 to be both prime to have a solution. Thanks to the previous section, we know p is some divisor of some 22n + 1.
We can rule out any divisor that is 2 mod 3. Since s itself is 2 mod 3, having p be 2 mod 3 forces k to be even, q to be 2 mod 3, and then 2kp + q – 4 to be a multiple of 3.
That leaves 3, or factors such as 6700417 of numbers at least 232 + 1. Matching one of these large factors to (2k – 2 ± 1) requires that k be 2 mod 32, and thus 2k is 4 mod 5. We know s is 1 mod 5, so s – 2k is 2 mod 5. For all possible ways that p and q can combine to be 2 mod 5, one of 2kp + q – 4 and p + 2kq – 4 ends up being a multiple of 5.
So if we protect against all k, our factors well and truly eliminate the possibility of (2k+2, a), even if a is composite.
Power-of-two Plus Power-of-three
We haven’t yet ruled out a power of two appearing on an otherwise protected k, in the pair (2k, 3r). That’s a power of two and a power of three. This has never appeared in any solution, although (8, 243) comes close. But we would need primes from 9 + 216 – 4 = 221 and 27 + 72 – 4 = 95, which are both composite. F(251) is 0.
Because our sum is 2 mod 3, the exponent k on 2 has to be odd, a departure from every pattern we have seen in this problem. Then we can examine everything mod 5 (remembering that s itself is 1 mod 5) and conclude that 3r – 2 + 9 × 2k – 4 will always be a multiple of 5. That constrains r to be only 1 or 2, where two factors cannot be moved over.
If s – 2k is exactly 3 or 9, then s – 2k will also be 3 or 9 mod 233 – 2. Using the fact that s itself is 232 – 5 mod 233 – 2, we can test out every k until we get periodic behavior. With such a kind modulus, we get periodic behavior after 32 iterations, and none of the values we land on are 3 or 9. If (2k, 3r) is ever a solution, the sum cannot be one that was protected using Fermat on k = 2.
These examples are fruitless, but our last edge case won’t be.
Fermat Factors and Edge Cases
“2ka × b can be factored equivalently as 2kb × a” has one other fail condition. b = a.
For that, we need s itself to be a multiple of a Fermat number!
If s can be written as (2k + 1)a, then the alternate factor sum we put all of our energy into covering, is just s itself. The pair of numbers is (2ka, a), and the product is 2k × a2. Assuming a is prime, the only other odd factor sum is 2k + a2. If this is 4 + p for some prime p, then the dialogue is possible and we know s is a solution.
However “we need s itself to be a multiple of a Fermat number” is somewhat restricting, given that we have so many Fermat requirements on s + 4 already. The big hammer forces us to place Fermat requirements on k = 1, 2, 4, 8, 16, and 32. In doing this, we lose the ability to use the Chinese Remainder Theorem with remainder 0, on any Fermat number that is not a multiple of 64. So, necessarily, all of these solutions take the form (264kp, p). But with this in mind, they are not so difficult to find.
Real Big Solutions
Using Chinese Remainder Theorem, we have that any number of the form 448578159043092819474671860342300540211 + 680564733841876926926749214863536422910n is protected via big hammer from all k, and is a multiple of 264 + 1. Filtering through the first 1000 of these for numbers which are (264 + 1)p for prime p and for which p2 + 264 – 4 is prime, we find three cases:

The corresponding primes are
- 8288458815750082591603
- 12494316464555860359823
- 29723575429400581568233
And the sums, which are the primes multiplied by 264 + 1, are
- 152895078539623524451066495989774459272051
- 230479458197597494120715906484217611483791
- 548303188901754018995507789825489120982761
These are the first of many solutions to have the form (264p, p). Of course, these are much smaller than 24534, so we are not yet in the end game. But the method used to find them can be applied at any magnitude, even in the presence of the big hammer. In fact, I believe these comprise the vast majority of all solutions.
The Rest of Infinity
I don’t have the tools to prove anything, especially given how one of the core results of this blog post is a pattern breaking down. However, as I understand it, unless precision coverings with Mersenne condition on k = 4 return, then the only way it is remotely likely to have F(s) = 1 as s grows unbounded, is to have Fermat protection against k = 1, 2, 4, 8, and 16, using the 5 Fermat primes. This means that s is necessarily going to be 232 – 5 mod 233 – 2. Further protections can be Fermat or Mersenne, and use factors of the next 22n + 1 rather than the whole thing, but there is no opportunity to depart from that base congruence.
By letting large powers of two remain uncovered, we can get clusters of solutions that look like (22na, b) or (22n+2, a) where n ≥ 6. These all have to have sums within a small range beyond 22n itself, so are relatively sparse. That said, I believe there should be infinitely many of them.
Much denser are the solution pairs (264ka, a) which need only the base congruence and one additional Fermat divisor. They can arise from as few as 2 successful prime checks. Since for each k, the valid a have constant density in the integers, and a prime check on a and on a2 + 264k – 4 is typically sufficient to prove a solution, we can estimate the density of solutions.
Return to Statistics
We can compute that 1 in 264 – 1, or 5.4 × 10-20 integers are capable of satisfying all of the congruences needed to be a. This number is independent of k. Those integers that are capable as a, have the added benefit of being guaranteed not divisible by 2, 3, 5, or several higher factors. Statistically speaking, only the first 3 are worth accounting for. So the probability an integer a both satisfies all the congruences and is prime, looks like 5.4 × 10-20 × 2 × 3/2 × 5/4 × 1/log(a) ≈ 2 × 10-19 / log(a).
Then moving to a2 + 264k – 4, let’s assume that a2 ≫ 264k – 4. For any fixed k, this will eventually be true. This number is also guaranteed not divisible by 2, 3, and 5. The probability it is prime looks like 2 × 3/2 × 5/4 × 1/log(a2). Moving the 2 out of the logarithm and multiplying by our earlier expression, we have 4 × 10-19 / log(a)2.
In Practice
The magnitude of s depends on both a and k, but let’s fix k = 1 now. Looking at 1000 digit numbers for s, we want 980 digit numbers for a. Using our density expression, we would expect about one in 1025 of them to yield a solution. That’s some 10955 solutions in the range where we couldn’t find any using other techniques!
Of our original 3141 small solutions, 8 of them look like (2ka, a):
- (1552, 97) = (24 × 97, 97)
- (3328, 13) = (28 × 13, 13)
- (23152, 1447) = (24 × 1447, 1447)
- (32512, 127) = (28 × 127, 127)
- (41872, 2617) = (24 × 2617, 2617)
- (293872, 18367) = (24 × 18367, 18367)
- (387952, 24247) = (24 × 24247, 24247)
- (455152, 28447) = (24 × 28447, 28447)
This meager group becomes the most inescapable kind of solution. These small examples don’t have the same requirement for total big hammer protection; all but (28 × 13, 13) make do with Mersenne k = 4, hence their sums ending in a 9. But as our expectations soar off to infinity, these solutions keep coming back, at every magnitude, forever.
A Proof
If I’m going to end this post, I want to attempt to prove one gargantuan solution to the puzzle. We will have our thousand digit solution, so help me.
I’ll use the Fermat number 23200 + 1. This exponent is 50 × 64, so it should be fair game. To get the digit count right, we need a 36 digit prime for a. Given our density estimate, there should be plenty of these. With a bit of code, I found one that works.

The Claim
The prime is 505840822837513381420917875816788723.
The actual sum, which is the prime times 23200 + 1, is as follows:
1000000000001351524183264572297770570158333992920185599829455174422223560591310263372183552852538759475774873472975281402193385637230054158093403908183277734433860294173522520003095104847965120774402019487257612695270203247159081120435980787389462386254142139326889658912470460982264865634478542037800961793070967187626521845790349448707099360189395609314697753579198359759816500384364492548664711065056648887898191927620487918344523711429771911431262337605356576691537595740771885990854872942604310495838097323173600550697834398288629666635535389611113402661323411583498835882366536172425416554745699468549269404624935054945390628748130271373989291727185752431104028756679241853505971264024995022405169664712766583488641464776657884263696846172404178224931176806000312607479629030019538968664803730983996030210322483405612316379581187150858285234590878498070715870694056634720257181680554621937745880563090412313376812926173137095122302868445331666802246444086083074396692273748401813266183762211571
That’s 1000 digits, right on the nose. I claim this is a solution.
Sam Says “you don’t know”
The sum shown is odd, not a multiple of 3, and subtracting 4 gives a composite number (one divisor is 641). Accordingly, Sam can claim with certainty that the product of any pair of numbers summing to this sum, has multiple valid factorizations.
Polly Says “that was true, but now I do”
The product Polly is told in this case, is 23200 × 5058408228375133814209178758167887232. There are 4800 distinct factorizations of this product into two factors both greater than or equal to 3. However, only 2 of these factorizations have an odd factor sum. Assuming the Goldbach Conjecture, every even factor sum can separately be expressed as the sum of two primes, and after Sam’s statement, Polly can throw those factorizations out. Of the two odd factor sums, one of them (23200 + 5058408228375133814209178758167887232) is 4 + p for a prime p. If Sam had this sum, they could not have claimed with certainty that Polly didn’t know the numbers, as 4p would factor uniquely. Therefore, in response to Sam’s statement, Polly determines that the numbers must be 505840822837513381420917875816788723 and 23200 × 505840822837513381420917875816788723.
Sam Says “now I do too”
Now for the fun part. Sam has to deduce the numbers from Polly’s reveal. To prove this, we start by noticing that the sum is 6705290747541849491 mod 265 – 2. As proven in the previous blog post, this means that for any pair of numbers 2ka and b which add to this sum, 2kb + a (with b exchanged for a to make a new sum) is not a multiple of 3, and 2kb + a – 4 is composite with known factors. Because of this, every such pair of summands would remain ambiguous to Polly despite Sam’s reveal.
The new sum 2kb + a is not relevant if b = a or a = 1. This constitutes a modest number of cases that we need to examine. For a = 1, k > 2, we use the logic in “power-of-two plus prime” and “power-of-two plus composite”. For a = 1, k = 2, we know s = 4 + 641n for some large n. The alternate factor sum n + 4 × 641 has the necessary property to make Polly’s statement impossible. Lastly, s cannot be written as 2k + 3r.
All that remains are the cases where s = 2ka + a. Here three such k exist: 128, 640, and 3200. In all three cases, one other possible factor sum is 2k + a2. For k = 128 and k = 640, this factor sum has the necessary property to make Polly’s statement impossible. But for k = 3200, Polly gets the answer. Sam, therefore, can deduce that of the 5 × 10998 different pairs of numbers that add up to this s, there is exactly one where Polly’s statement is possible. Sam knows the numbers.
Q.E.D.?
Our big hammer technique simplifies proofs a lot. However, there are still a couple of ways this proof could be wrong. I assumed the Goldbach Conjecture rather than systematically finding a pair of odd primes adding to every relevant even number. I used “probable prime” tests to conclude that certain large numbers were prime. Nevertheless, I am quite confident that the value described is a solution to the puzzle. It is part of a family of solutions of the form (264kp, p). I’m even willing to state my confidence that all 10975 or so of the 1000 digit solutions belong to this family.
I was extremely inspired to write this post, on something of a whim. Much of the research for it was done close to 2 years ago. By writing this, I’ve again communicated the extent of my knowledge about this so-called impossible puzzle. However, that extent may grow whenever the fixation returns! I may come back and try to present the same material again with more illustrations or animations some day. Whether or not I do that, thank you for reading.